а)
Строим координатную прямую и отмечаем на ней закрашенными точками 1\6 и 1
Получается, что х принадлежит [1\6;1]
Снова строим координатную прямую и отмечаем на неё закрашенную точку 3\4. Получаем, что х принадлежит
3) Общий
Отмечаем на координатной прямой все точки 1\6, 3\4 и 1.
Совмещаем графики и получаем решение системы уравнений.
x принадлежит [1\6;\3\4]
Напоминаю, что вид скобок имеет значение.
б)
Строим координатную прямую и отмечаем на ней выколотые точки 0 и 5. х принадлежит
2) х>2
Строем координатную прямую с выколотой точкой 2 и получаем, что х принадлежит
Объединяем значения на координатной прямой и получаем решение системы уравнений. х принадлежит
Первый коофициент этого уравнения отличен от нуля (1≠0)
1) Чтобы квадратное уравнение имело корни, нужно чтобы его дискриминант не был отрицательным:
Д = (-2а + 6)² - 4 * 1 * (10 - 6а) = (6 - 2а)² - 4 * 1 * (10 - 6а) = 36 - 24а + 4а² - 40 + 24а =4а² - 4
4а² - 4 ≥0
4а² ≥ 4
а² ≥ 1
ответ: при а ≥ 1 и а ≤ -1,
2) Чтобы уравнение имело корни одного знака нужно чтоб его свободный член был > 0:
так как х² с коофициентом 1 , то ⇒ 10 - 6а > 0
В результате получаем систему^
{ а ≥ 1,
{ а ≤ -1, ⇒
{10 - 6а > 0;
{ - 6а > -10 | : (-6)
{a < 10/6
{a < 5/3
Нарисуем эти неравенства на числовой оси (смотри риссунок-вложение) и будем иметь:
а ∈ (-∞;-1] U [1; 5/3)
P.S. Там где точки имеют пересечения линий и есть ответ.
Думаю, что все правильно, вообще параметры это тема не из легких.
а)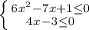
Строим координатную прямую и отмечаем на ней закрашенными точками 1\6 и 1
Получается, что х принадлежит [1\6;1]
Снова строим координатную прямую и отмечаем на неё закрашенную точку 3\4. Получаем, что х принадлежит![(-\infty;\frac{3}{4}]](/tpl/images/0077/2198/d1207.png)
3) Общий
Отмечаем на координатной прямой все точки 1\6, 3\4 и 1.
Совмещаем графики и получаем решение системы уравнений.
x принадлежит [1\6;\3\4]
Напоминаю, что вид скобок имеет значение.
б)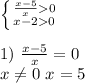
Строим координатную прямую и отмечаем на ней выколотые точки 0 и 5. х принадлежит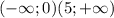
2) х>2
Строем координатную прямую с выколотой точкой 2 и получаем, что х принадлежит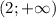
Объединяем значения на координатной прямой и получаем решение системы уравнений. х принадлежит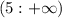
Первый коофициент этого уравнения отличен от нуля (1≠0)
1) Чтобы квадратное уравнение имело корни, нужно чтобы его дискриминант не был отрицательным:
Д = (-2а + 6)² - 4 * 1 * (10 - 6а) = (6 - 2а)² - 4 * 1 * (10 - 6а) = 36 - 24а + 4а² - 40 + 24а =4а² - 4
4а² - 4 ≥0
4а² ≥ 4
а² ≥ 1
ответ: при а ≥ 1 и а ≤ -1,
2) Чтобы уравнение имело корни одного знака нужно чтоб его свободный член был > 0:
так как х² с коофициентом 1 , то ⇒ 10 - 6а > 0
В результате получаем систему^
{ а ≥ 1,
{ а ≤ -1, ⇒
{10 - 6а > 0;
{ а ≥ 1,
{ а ≤ -1, ⇒
{ - 6а > -10 | : (-6)
{ а ≥ 1,
{ а ≤ -1, ⇒
{a < 10/6
{ а ≥ 1,
{ а ≤ -1, ⇒
{a < 5/3
Нарисуем эти неравенства на числовой оси (смотри риссунок-вложение) и будем иметь:
а ∈ (-∞;-1] U [1; 5/3)
P.S. Там где точки имеют пересечения линий и есть ответ.
Думаю, что все правильно, вообще параметры это тема не из легких.