Дана функция f : R ->R,(f)x=-3x-1 дополните:
А([];-5)єG
B(-2;[])єG
постройте график функции​

Я НАПИШУ АЛГОРИТМ И ТЫ ПО НЕМУ РЕШИШЬ КАЖДОЕ УРАНЕНИЕ.

уравнение имеет вид ах в квадрате+вх+с=0.

нужно найти дискриминант. он ищется по формуле D=в в квадрате- 4ас.

если дискриминант отрицательное число, то крней нет, если положительный, то корня 2, если равен 0, то корень1.

далее ищем корни.

х1=-в+ корень из дикриминанта\ 2а

х2= -в-корень из дискриминанта\2а.

ВАЖНО ПОМНИТЬ, что запись -в предусматривает в с противополодным знаком. например в уравнении у тебя дано вместо в 5. в формулу корней подставляешь -5, а если дано -5, то в формулу пишешь 5.

Событие А- "студент ответил хотя бы на 1 из 2 вопросов" значит, что студент ответил на один вопрос или на два.

Испытание состоит в том, что из 20-ти вопросов выбирают два.

n=C²₂₀=20!/((20-2)!·2!)=190

Событие M- "студент ответил на 1 из 2 вопросов"

Событию М благоприятствуют те случаи, когда один вопрос выбран из 16-ти выученных, а второй вопрос из четырех невыученных.

m=C¹₁₆·C¹₄=16·4=64

По формуле классической вероятности

p(M)=m/n=   -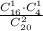

вероятность того, что студент ответил на один вопрос из двух

Событие N- "студент ответил на 2 из 2 вопросов"

Событию N благоприятствуют те случаи, когда два вопроса выбраны из 16-ти выученных.

m=C²₁₆·C⁰₄=16!/((16-2)!·2!)=120

По формуле классической вероятности

p(N)=m/n=   -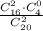

вероятность того, что студент ответил на два  вопроса из двух.

р(А)=p(M)+p(N)=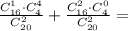

Событие В- "студент не ответил хотя бы на 1 из 2 вопросов", значит не ответил на один или не ответил на два.

Событие M- "студент ответил на 1 из 2 вопросов" означает, что на один ответил, а на другой не ответил.

p(M)=m/n=   -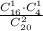

Событие K- "студент не ответил на 2 из 2 вопросов"

Событию N благоприятствуют те случаи, когда два вопроса выбраны из 4-х невыученных.

m=C⁰₁₆·C²₄=4!/((4-2)!·2!)=6

По формуле классической вероятности

p(K)=m/n=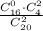  

p(B)=p(M)+p(K)=