2) График в первом вложении. Во втором вложении заштрихована площадь фигуры, которую нужно найти. Так как нам не дан конкретный отрезок, она ограничивается вертикальными прямыми, проведенными через точки пересечения графиков - х = 1 и х = 5.
График функции y = 6 - x выше графика функции y = 5/x, поэтому формулу площади фигуры составляем следующим образом:
3) График в третьем вложении. В четвертом вложении заштрихована площадь фигуры, которую нужно найти. Так как нам дан только 1 конец отрезка, которым ограничена фигура, вторым концом будет точка пересечения графиков функций - х = 1.
График функции y = 4x + 1 на отрезке [1; 2] выше графика функции y = 5/x, поэтому формулу площади составляем следующим образом:
Пронумерую места на скамейке от 1 до 5, нумерация слева направо. Общее число вариантов рассадки относительно этих мест = 5! = 5*4*3*2*1 = 120 (на первое место могут сесть 5 человек, на второе - 4, т.к. кто-то уже сидит, и т.д.).
Пусть первая девочка сидит левее второй. Тогда если они сидят вместе, то на местах соответственно: 1 и 2, 2 и 3, 3 и 4, 4 и 5 - 4 варианта. Для каждого варианта есть 3! = 6 вариантов рассадки мальчиков (девочки зафиксированы на своих местах). Тогда суммарно в этом случае будет 4*6 = 24 подходящих случая. Если они поменяются местами - это ещё 24 варианта, итого 48 нужных вариантов из 120, т.е. вероятность равна = 0,4.
ответ: 2) 12 - 5ln 5; 3)7 - 5ln2.
Объяснение:
2) График в первом вложении. Во втором вложении заштрихована площадь фигуры, которую нужно найти. Так как нам не дан конкретный отрезок, она ограничивается вертикальными прямыми, проведенными через точки пересечения графиков - х = 1 и х = 5.
График функции y = 6 - x выше графика функции y = 5/x, поэтому формулу площади фигуры составляем следующим образом:
3) График в третьем вложении. В четвертом вложении заштрихована площадь фигуры, которую нужно найти. Так как нам дан только 1 конец отрезка, которым ограничена фигура, вторым концом будет точка пересечения графиков функций - х = 1.
График функции y = 4x + 1 на отрезке [1; 2] выше графика функции y = 5/x, поэтому формулу площади составляем следующим образом:
0,4
Объяснение:
Пронумерую места на скамейке от 1 до 5, нумерация слева направо. Общее число вариантов рассадки относительно этих мест = 5! = 5*4*3*2*1 = 120 (на первое место могут сесть 5 человек, на второе - 4, т.к. кто-то уже сидит, и т.д.).
Пусть первая девочка сидит левее второй. Тогда если они сидят вместе, то на местах соответственно: 1 и 2, 2 и 3, 3 и 4, 4 и 5 - 4 варианта. Для каждого варианта есть 3! = 6 вариантов рассадки мальчиков (девочки зафиксированы на своих местах). Тогда суммарно в этом случае будет 4*6 = 24 подходящих случая. Если они поменяются местами - это ещё 24 варианта, итого 48 нужных вариантов из 120, т.е. вероятность равна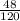
= 0,4.