Рассмотрим уравнене -х³-х²+13х-10=0 по теореме Безу , если а -корень корень многочлена , то многочлен делится на двучлен (х-а) , в нашем случае сумма коэффифциентов равна -1+(-2)+13+(-10)=0 , значит одним из корней является х=1 ⇒ весь многочлен -х³-х²+13х-10=0 делится на (х-1) для удобства деления вынесем за скобку общий множитель (-1)
1) 1-я бригада выполняет задание за 40 дней, 2-я бригада - за 10 дней
2) 1-я бригада выполняет задание за 12 дней, 2-я бригада - за 24 дня.
Объяснение:
Пусть С - объём производственного задания
х - время, за которое задание выполняет 1-я бригада
у - время за которое задание выполняет 2-я бригада
По условию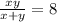
(1)
По условию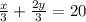
⇒ x + 2y = 60 ⇒ x = 60 - 2y (2)
Подставим (2) уравнение в (1)
60y - 2y² = 480 - 8y
2y² - 68y + 480
y² - 34y + 240 = 0
D = 34² - 4 · 240 = 196
√D = 14
y₁ = 0.5(34 - 14) = 10 (дней) х₁ = 60 - 2 · 10 = 40 (дней)
у₂ = 0,5(34 + 14) = 24 (дня) х₂ = 60 - 2 · 24 = 12 (дней)
по теореме Безу , если а -корень корень многочлена , то многочлен делится на двучлен (х-а) , в нашем случае сумма коэффифциентов равна
-1+(-2)+13+(-10)=0 , значит одним из корней является х=1
⇒ весь многочлен -х³-х²+13х-10=0 делится на (х-1)
для удобства деления вынесем за скобку общий множитель (-1)
-1(х³+2х²-13х+10)=0
х³+2х²-13х+10 | x -1
- x³- x² |
| x² +3x -10
3x²-13x
- 3x²-3x
-10x+ 10
- (-10x)+10
0
Итак: -х³-х²+13х-10 = -1*(х-1)*(x² +3x -10)