Дана функция y=(x−128)2−13.
Для построения графика данной функции необходимо перейти к вс системе координат. Запиши координаты новой начальной точки.

пусть 
из первого бидона (3%) взяли X л молока, 
количество жира Ж1 = x *3%/100% = 0,03x л
тогда из условия следует, что
из второго бидона (6%) взяли  (9 - X) л молока
количество жира Ж2 = (9-x) *6%/100% = 0,06(9-x) л
тогда из условия следует, что
в смеси
количество жира Ж = 9 *5%/100% = 9 * 0,05 = 0,45 л
количество жира не изменилось
составим уравнение
Ж1 +Ж2 =Ж
0,03x +0,06(9-x) = 0,45
3x + 6(9-x) =45
x +2(9-x) = 15
x = 3 л
9 - x = 9-3 =6 л

ответ
из первого бидона (3%) взяли 3 л молока

из второго бидона (6%) 6 л молока

Решением является перебор вариантов:

Можно достать шары из урны четырьмя

1) 2 белых

2) 2 чёрных

3) 1 белый и 1 чёрный

4) сначала 1 чёрный, потом 1 белый.

Вероятности этих событий:

1)  

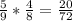
2)  

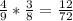
3)  

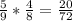
4)  

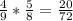
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:

Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:

Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.