Дана некоторая тройка чисел. c любыми двумя из них разрешается проделывать следующее: если эти числа равны a и b, то их можно заменить на a+b/√2 и a−b/√2. mожно ли с таких операций получить тройку 1, √2, 1-√2 из тройки 2, √2, 1/√2? , !
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.
1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔
Тогда
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔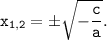
Тогда
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.
13 000 рублей
Объяснение:
Костюм на 4000 р дороже, чем футболка, значит 4 костюма стоят как 4 футболки плюс 4×4000 = 4 футболки + 16 000
По условиям 4 костюма и 2 футболки стоят 70 000. Значит 4 футболки + 16 000 + 2 футболки = 70 000
4 футболки + 16 000 + 2 футболки = 4 футболки + 2 футболки + 16 000 = 6 футболок + 16 000
Значит 6 футболок + 16 000 = 70 000
Значит 6 футболок = 70 000- 16 000 = 54 000
Значит она футболка стоит 54 000 ÷ 6 = 9 000
А костюм на 4000 дороже - значит он стоит 9000+4000=13 000 рублей