Всего вариантов ровно 1000: от 000 до 999. Чтобы их перебрать все, нужно 4000 сек. 1) Если известно 3 цифры, но неизвестно в каком порядке, то всего 6 вариантов кода: abc, acb, bac, bca, cab, cba. Чтобы их перебрать, нужно 4*6 = 24 секунды. 2) Если известна только одна цифра а, то есть 300 вариантов: от а00 до а99 - 100 вариантов, от 0а0 до 9а9 - 100, и от 00а до 99а - 100. Но, когда мы проверяем варианты от 0а0 до 9а9, то первую цифру а можно пропустить, потому что мы ее уже проверили от а00 до а99. Остается 9*10 = 90 вариантов. А когда мы проверяем от 00а до 99а, то можно пропустить и первую, и вторую цифру а. Остается 9*9 = 81 вариант. Таким образом, остается не 300, а 100+90+81=271 вариант. Это займет 271*4 = 1084 секунды. 3) Сумма трех чисел кода нечетная. Сумма может быть от 0+0+0=0 до 9+9+9=27, всего 28 вариантов, из них 14 четных и 14 нечетных. Значит, сумма будет нечетной в половине случаев. Чтобы их перебрать, нужно 4000/2 = 2000 секунд.
Часть А
Задание 1
а) (2а-а²)-(а²+2а-7) = 2а-а²+а²-2а+7 = 7
б) (1-у)3х²у-(3ху-х)ху = ху(3х-3ху-3ху+х) = ху(4х-6ху) = 2х²у (2-3у)
Задание 2
9^6 - 3^10 = 3^7 - 3^10 = 3^-3 : 24 =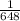
Задание 3
а) 27t²-3t = 0
3³t²-3t = 0
3²t = 0
9t = 0
t = 0
б) 4х²-2х-4х²+8х=4
6х = 4
х =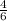 =
= 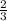
в)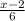 -
- 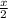 = 2
= 2
х-2 -3х = 12
-2х = 14
х = -7
Часть В
1) Пусть х деталей в час изготавливал ученик, тогда мастер -- (х+6) дет в час. Составляем уравнение по условию задачи:
8х=5(х+6)
8х=5х+30
8х-5х=30
3х=30
х=10 ( дет) в час изготавливал ученик
10+6=16 дет в час изготавливал мастер
Объяснение:
Подробное решение и есть объяснение, можно лучший ответ?
Чтобы их перебрать все, нужно 4000 сек.
1) Если известно 3 цифры, но неизвестно в каком порядке, то всего 6 вариантов кода: abc, acb, bac, bca, cab, cba.
Чтобы их перебрать, нужно 4*6 = 24 секунды.
2) Если известна только одна цифра а, то есть 300 вариантов:
от а00 до а99 - 100 вариантов, от 0а0 до 9а9 - 100, и от 00а до 99а - 100.
Но, когда мы проверяем варианты от 0а0 до 9а9, то первую цифру а можно пропустить, потому что мы ее уже проверили от а00 до а99.
Остается 9*10 = 90 вариантов.
А когда мы проверяем от 00а до 99а, то можно пропустить и первую, и вторую цифру а. Остается 9*9 = 81 вариант.
Таким образом, остается не 300, а 100+90+81=271 вариант.
Это займет 271*4 = 1084 секунды.
3) Сумма трех чисел кода нечетная. Сумма может быть от 0+0+0=0 до 9+9+9=27, всего 28 вариантов, из них 14 четных и 14 нечетных.
Значит, сумма будет нечетной в половине случаев.
Чтобы их перебрать, нужно 4000/2 = 2000 секунд.