1) по теореме косинусов имеем: a² = b² + c² - 2bc cos a = 25 - 24 cos 135° = 25 + 12√2 a = √(25 + 12√2) по теореме синусов, a / sin a = b / sin b sin b = sin a · b / a = √2 / 2 · 3 / √(25 + 12√2) = 3 / √(50 + 24√2) ∠b = arcsin(3 / √(50 + 24√2)) ∠c = 180° - 135° - ∠b = 45° - arcsin(3 / √(50 + 24√2)) 2) ∠a = 180° - ∠b - ∠c = 65° по теореме синусов b / sin b = a / sin a b = a sin b / sin a = 24.6 · √2 / 2 / (sin 65°) = 123√2 / (10 sin 65°) по теореме синусов c / sin c = a / sin a c = a sin c / sin a = 24.6 ·sin 70° / sin 65°
а) две точки пересечения (два корня)
b)
Объяснение:
a)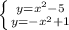
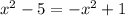в) 
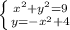окружность R=3, O(0;0) и
б) xy=3 или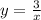
гипербола, точка симметрии (0;0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы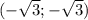
и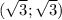 
у окружност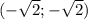и
и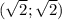 
г)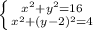
это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.