Здесь всё однозначно. 1 - лжец, он солгал: ДО него было 0 истинных и 0 ложных. 0 + 2 ≠ 0, это истина. 2 - лжец, он солгал: до него было 1 ложное и 0 истинных. 0 + 2 ≠ 1. 3 - рыцарь, он сказал правду: до него было 2 ложных и 0 истинных. 0 + 2 = 2. 4 - лжец, 2 ложных и 1 истинное, 1 + 2 ≠ 2. 5 - рыцарь, 3 ложных и 1 истинное, 1 + 2 = 3 6 - лжец, 3 ложных и 2 истинных, 2 + 2 ≠ 3 7 - рыцарь, 4 ложных и 2 истинных, 2 + 2 = 4 И дальше точно также, через одного. 8 - лжец, 9 - рыцарь, 10 - лжец, 11 - рыцарь, 12 - лжец, 13 - рыцарь. Рыцарей 6, лжецов 7.
Теорема. Конечное объединение счетных множеств дает счетное множество.
По сути нужно доказать, что и и являются счетными. Докажем счетность множества .
Очевидно, что между каждым элементом множества можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество - счетно.
Докажем теперь счетность множества
Согласно основной теореме алгебры, полином -ой степени имеет различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество - счетно.
1 - лжец, он солгал: ДО него было 0 истинных и 0 ложных.
0 + 2 ≠ 0, это истина.
2 - лжец, он солгал: до него было 1 ложное и 0 истинных.
0 + 2 ≠ 1.
3 - рыцарь, он сказал правду: до него было 2 ложных и 0 истинных.
0 + 2 = 2.
4 - лжец, 2 ложных и 1 истинное, 1 + 2 ≠ 2.
5 - рыцарь, 3 ложных и 1 истинное, 1 + 2 = 3
6 - лжец, 3 ложных и 2 истинных, 2 + 2 ≠ 3
7 - рыцарь, 4 ложных и 2 истинных, 2 + 2 = 4
И дальше точно также, через одного.
8 - лжец, 9 - рыцарь, 10 - лжец, 11 - рыцарь, 12 - лжец, 13 - рыцарь.
Рыцарей 6, лжецов 7.
Теорема. Конечное объединение счетных множеств дает счетное множество.
По сути нужно доказать, что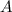 и
и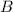 
являются счетными. Докажем счетность множества 
.
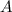Очевидно, что между каждым элементом множества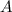
можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество 
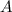- счетно.
Докажем теперь счетность множества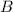
Согласно основной теореме алгебры, полином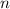
-ой степени имеет 
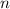различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество 
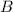- счетно.
Следовательно,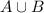
- счетно.