Дано трикутник ABC. Внаслідок паралельного перенесення точку A1, симетричну в точці В відносно початку координат. У які точки внаслідок такого перенесення переходять вершини A, B, C, якщо A(-3;1) B(-2;4) і C(3;-1)? Відповідь записати у вигляді приклада A1(1;1) B1(2;2) C1(3;3)
Правильно я условия записал?
1)
Вот и получается: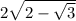
2)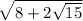 использую формулу
использую формулу 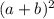
получаем: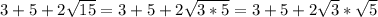 дальше расставляем это так:
дальше расставляем это так: 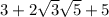 и получаем формулу:
и получаем формулу: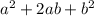 сводим уравнение получается:
сводим уравнение получается: 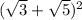 .
.
Теперь не забываем, что у нас есть корень ещё один, который мы убрали, на время и получаем: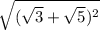 , квадрат корней сокращается и получается:
, квадрат корней сокращается и получается: 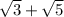
3²⁰¹⁹
3ˣ заканчивается на 3, 7, 9, 1 (всего 4 варианта)поэтому делим 2019 на 4 и находим остаток:
2019:4=504+(3 остаток)
3 в степени остатка заканчивается на ту же цифру, что и 3²⁰¹⁹:
3³=27, заканчивается на 7, ⇒ 3²⁰¹⁹ заканчивается на 7
для реальных пацанов 3²⁰¹⁹=2031483405154295336973313472053084709260165132781091274133600590646801546062065765597065855075575559645927206954432480413186166405878164110031288954170986733309264050445838468504498778699177789361771869614187645674280996416481296555162675387948432660577927475570146993847223780848939997643825423577469203752422288212763865648689848881642972843094612947038314258546390369577705503447563072614262142286296939162007841741637816483019030536893460148101171782562064520251485785859119437328196648101903890701482615485865832441865716248873898106659137203306018261179152584687131580181305862988250432024498124432979731217593409111662715001322758910196435262171827223977525409867024424577485948514235081918022945654217156396051056847793728422425953481621244536777888697666022911601660615917213688613387319271603000479001551126897575642846623706325654768983209005219684703673779251341850111123431449910486033100144688372851430572754366458936629186286950719322952375577741467
ответ: 7.