Пусть общий вид уравнения касательной: . Прямая будет касательным к графику функций (в данном случае к параболе), если она имеет одну общую точку.
-x² + 2x - 3 = kx + b ⇒ -x² + (2-k)x - 3 - b = 0 (1)
x² + 2 = kx + b ⇒ x² -kx + 2 - b = 0 (2)
Найдем дискриминант первого и второго уравнения
Графики имеют одну общую точку, если их дискриминант = 0.
По теореме Виета
Зная значения k, найдем коэффициент b.
Искомые касательные: y = -2x+1 и y = 4x-2.
Пусть общий вид уравнения касательной: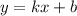 . Прямая будет касательным к графику функций (в данном случае к параболе), если она имеет одну общую точку.
. Прямая будет касательным к графику функций (в данном случае к параболе), если она имеет одну общую точку.
-x² + 2x - 3 = kx + b ⇒ -x² + (2-k)x - 3 - b = 0 (1)
x² + 2 = kx + b ⇒ x² -kx + 2 - b = 0 (2)
Найдем дискриминант первого и второго уравнения
Графики имеют одну общую точку, если их дискриминант = 0.
По теореме Виета
Зная значения k, найдем коэффициент b.
Искомые касательные: y = -2x+1 и y = 4x-2.