даны графики стоимости одной акции в рублях двух разных фирм инвестор изначально имеет 300 рублей. с какой наименьшей суммой он может остаться к третьему дню при самых неудачных покупках и продажи акций?

ймовірність того, що листочок ммістить цифру 2 дорівнює проте ймовірність того, що листок містить саме число 2 менша та дорівнює

Объяснение:

У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів

Тож подивимось скількі днів у місяці містять двійку:

це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,

як бачимо у кожному місяці високостного року по 12 днів із цифрою 2

тому на рік таких днів буде 12*12=144

а ймовірність такої події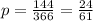

--------------------------

якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише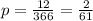 , оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме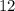

Решение: Используем геометрическое определение вероятности события AA = (Встреча с другом состоится).

Обозначим за хх и уу время прихода, 0≤х,у≤600≤х,у≤60 (минут). В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата ОАВСОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 13 минут, то есть

y−x<13,y>x,y−x<13,y>x,

x−y<13,x>y.x−y<13,x>y.

Этим неравенствам удовлетворяют точки, лежащие в области GG, очерченной красным. 

Тогда вероятность встречи равна отношению площадей области GG и квадрата, то есть

P(A)=SGSOABC=60⋅60−55⋅5560⋅60=23144=0,16.P(A)=SGSOABC=60⋅60−55⋅5560⋅60=23144=0,16.

ответ: 0,16

Объяснение:

отметь как лучший