Даны множества: Q= {1; 2; 3;…}, C={0; 0,3; 1; 1,3; 2}, A={-0,5; 0; 0,5}, B={1; 2; 3; 4; 5},
D= {…-1; -0,5; 0; 0,5; 1,…}.
Выясните:
1) Какое из двух множеств является подмножеством другого: а) Q или D; б) D или А; в) В или N.
2) а) Q ∩ C=?; Q ∩ А=?; Q ∩ В=?; Q ∩ D=?; A ∩ B=?; A ∩ D=?; B ∩ C=?; б) A ⋃ B; C ⋃ Q; C ⋃ B.
D ∈ [-5 ;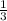
]
Объяснение:
D (Область определения) - это все х
По условию дано: y=√(5-14x-3x²)
корень можно извлекать из числа ≥ 0
Найдём при каких значениях икс 5-14x-3x² ≥ 0:
-3x²-14x+5 ≥ 0
3x²+14x-5 ≤ 0
D = b² - 4ac = 14² - 4*(-5)*3 = 196 + 60 = 256 = 16²
Применим метод интервалов:
расположим получившиеся корни на числовой прямой
+ _ +
--------------------5----------------------------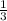
---------> x
Решением этого неравенства 3x²+14x-5 ≤ 0 является [-5 ;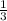
]
Транскрипт
Самостоятельный выбор профессии - это «второе рождение человека», поскольку от того,
насколько правильно выбран жизненный путь, зависят общественная ценность человека, его
место среди других людей, удовлетворенность работой, физическое и психическое здоровье,
радость. Хорошо, когда вы с детства мечтаете об определенной профессии- стать пиарщиком
или профессиональным спортсменом- и не сомневаетесь, что осуществите эту мечту. В этом случае
не возникнет проблем с выбором профессии. А остальным как поступить? У одних тинейджеров
пока нет никаких увлечений. Другие, наоборот , интересуются всем: одновременно занимаются в
спортивных секциях, посещают несколько кружков и факультативов. Им не хватает свободного
времени. Они очень активны и в учебе, и в общественной деятельности. И, как ни странно, уних все
везде получается! Но, к сожалению, и такие дети не могут определиться с тем, что им нравится
больше, с чем им связать свою дальнейшую жизнь. Стихийность выбора профессии нередко
приводит к неудовлетворенности человека своей жизнью. Работа становится неинтересной ,
что порой даже приводит к нервным срывам. Поэтому правильный выбор профессии- это
здоровье, удовлетворенность, творчество, успех и счастье.
1. Выбор профессии -это :
A) второе рождение человека
Б) жизненный путь
B) место среди других дюдей
Г) неудовлетворенность
Д) особый выбор
2. Какие увлечения утинейджеров ?
A) мало времени
Б) нет увлечений одновременно занимаются в нескольких спортивных секциях
Г) очень много свободного времени
Д) увлекается рыбалкой
3. Стихийность выбора профессии приводит к:
A) болезни
Б) нервным срывам
B) неудовлетворенности
Г) славе
Д) удовлетворенности
4. Из словаря синонимов найдите синонимы к ключевым словам.
Из дополнительных источников найдите материал о тинейджерах
Ключевые слова
Синонимы
5. Составьте простой план текста
2.
3.
6. Напишите изложение по прочитанному тексту, Используйте сложные предложения ,
выражающие условные, уступительные отношения
Объяснение: