Число А называется пределом функции y=f(x) при х стремящемся к а, если для любого е>0 найдётся такое δ=δ(е)>0, что для всех х , удовлетворяющих условию 0< |x-a|<δ ( то есть для х из δ-окрестности числа а ) выполняется неравенство |f(x)-A|<e ( то есть функция f(x) попадает в е-окрестность числа А ).
Причём сама ф-ция может быть не определена в самой точке х=а, но определена в окрестности этой точки.
Определение понимать можно так. Как только переменная х принимает значения, близкие к числу а (х-->a), то функция принимает значения, близкие к числу А ( f(x)-->A ).
Напримеp, .
Возьмём значения переменной х ,близкие к числу 2.
Пусть х=1,9 , тогда вычислим значение ф-ции у(1,9)=х+1=1,9+1=2,9≈3
Как видно ,при стремлении переменной к числу 2 справа ( числа больше 2) или слева (числа меньше 2) значения ф-ции у=х+1 всё ближе и ближе подходят к числу 3.
В этом примере х=2 входит в область определения ф-ции, поэтому можно подсчитать значение ф-ции при х=2.Это будет у(2)=2+1=3.
Можно рассмотреть случаи, когда х--->∞.Но там всё аналогично.При удалении переменной х от начала координат, функция начинает принимать значения, близкие к А.Например,
Представьте график гиперболы у=1/х.Как только переменная удаляется по оси ОХ вправо или влево, то график ф-ции приближается к самой оси ОХ .А ось ОХ - это прямая, уравнение которой у=0. Предельное значение ф-ции - ноль, хотя сама ф-ция никогда не может достигнуть значения 0.
Можно разбирать ещё много различных случаев вычисления предела ф-ции.Может, немного стало яснее, что это такое?
Число А называется пределом функции y=f(x) при х стремящемся к а, если для любого е>0 найдётся такое δ=δ(е)>0, что для всех х , удовлетворяющих условию 0< |x-a|<δ ( то есть для х из δ-окрестности числа а ) выполняется неравенство |f(x)-A|<e ( то есть функция f(x) попадает в е-окрестность числа А ).
Причём сама ф-ция может быть не определена в самой точке х=а, но определена в окрестности этой точки.
Определение понимать можно так. Как только переменная х принимает значения, близкие к числу а (х-->a), то функция принимает значения, близкие к числу А ( f(x)-->A ).
Напримеp,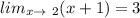 .
.
Возьмём значения переменной х ,близкие к числу 2.
Пусть х=1,9 , тогда вычислим значение ф-ции у(1,9)=х+1=1,9+1=2,9≈3
х=1,99 ⇒ у(1,99)=2,99≈3
х=1,999 ⇒ у(1,999)=2,999≈3
..........................................................
х=2,1 ⇒ у(2,1)=2,1+1=3,1≈3
х=2,01 ⇒ у(2,01)=3,01≈3
х=2,001 ⇒ у(2,001)=3,001≈3
Как видно ,при стремлении переменной к числу 2 справа ( числа больше 2) или слева (числа меньше 2) значения ф-ции у=х+1 всё ближе и ближе подходят к числу 3.
-------------------------(2)-------------------------
слева -----> <------ справа
В этом примере х=2 входит в область определения ф-ции, поэтому можно подсчитать значение ф-ции при х=2.Это будет у(2)=2+1=3.
Можно рассмотреть случаи, когда х--->∞.Но там всё аналогично.При удалении переменной х от начала координат, функция начинает принимать значения, близкие к А.Например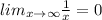 ,
,
Представьте график гиперболы у=1/х.Как только переменная удаляется по оси ОХ вправо или влево, то график ф-ции приближается к самой оси ОХ .А ось ОХ - это прямая, уравнение которой у=0. Предельное значение ф-ции - ноль, хотя сама ф-ция никогда не может достигнуть значения 0.
Можно разбирать ещё много различных случаев вычисления предела ф-ции.Может, немного стало яснее, что это такое?