Объяснение:
5) 5x - 2(2x-8)≥0
5x - 4x - 16 ≥0
x ≥ 16
ответ: x ∈ [ 16; + ∞)
6)
x ∈ [ -6; -3]
ответ: -3
7)
a) 16 - x^2 ≤0
(4-x)(4+x) ≤ 0
Нули функции:
4 - x = 0 4 + x = 0
x = 4 x = -4
(Тут строишь прямую, да и в принципе во всех предыдущих заданиях тоже)
(Будет что-то типа такого)
- -4 + 4 - >x (методом интервалов находим нужный нам промежуток)
ответ: x ∈ ( -∞; -4]∪[4;+∞)
б)(x+3)(5x-10)> 0
нули ф.
x +3 = 0 5x - 10 = 0
x = -3 x = 2
+ -3 - 2 + >x (так же методом интервалов)
ответ: x ∈ ( - ∞; -3)∪(2; +∞)
9) О.Д.З
x+1≥0
x²+2x-15 = 0 x ≥ -1
D = 2²-4*1*(-15) = 64
(можешь дальше дискриминантом решать)
По т. Виета:
x(1) + x(2) = -b = -2 ; x(1) = -5 - не уд. усл. О.Д.З
x(1)*x(2)=c = -15 ; x(2) = 3
ответ: 3
Объяснение:
5) 5x - 2(2x-8)≥0
5x - 4x - 16 ≥0
x ≥ 16
ответ: x ∈ [ 16; + ∞)
6)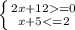
x ∈ [ -6; -3]
ответ: -3
7)
a) 16 - x^2 ≤0
(4-x)(4+x) ≤ 0
Нули функции:
4 - x = 0 4 + x = 0
x = 4 x = -4
(Тут строишь прямую, да и в принципе во всех предыдущих заданиях тоже)
(Будет что-то типа такого)
- -4 + 4 - >x (методом интервалов находим нужный нам промежуток)
ответ: x ∈ ( -∞; -4]∪[4;+∞)
б)(x+3)(5x-10)> 0
нули ф.
x +3 = 0 5x - 10 = 0
x = -3 x = 2
+ -3 - 2 + >x (так же методом интервалов)
ответ: x ∈ ( - ∞; -3)∪(2; +∞)
9)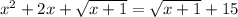 О.Д.З
О.Д.З
x²+2x-15 = 0 x ≥ -1
D = 2²-4*1*(-15) = 64
(можешь дальше дискриминантом решать)
По т. Виета:
x(1) + x(2) = -b = -2 ; x(1) = -5 - не уд. усл. О.Д.З
x(1)*x(2)=c = -15 ; x(2) = 3
ответ: 3