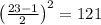Дайте ответ такой как должен быть на скрине

1.Весь обьем работы принимаем за 1.
2. Х - это время за которое всю работу сам выполнит 1 слесарь
3. Y - это время за которое всю работу сам выполнит 2 слесарь

Так как второй на 1 час=60 минут дольше, то первое уравнение системы

y - x = 60

Составляем второе уравнение:

1. Так как вся работа - это 1, то 1 слесарь за 1 минуту выполняет 1/x часть работы а второй за 1 минуту - 1/y часть работы

2. Работают вместе

1 слесарь 45 минут - значит всего выполнил работы - 1/x × 45

2 слесарь 45 минут и еще 2 часа 15 минут Итого работает 3 часа= 180 минут

Значит выполнил 1/y × 180 часть работы

вся работа - 1

уравнение получается:

1/x×45 + 1/y × 180 = 1
Решаем систему

Вышлю фото при необходимо сти.

При решении системы получается квадратное уравнение
x^2 - 165x - 2700=0
x = 180

Тогда y = 180+60= 240

ответ: 1 слесарь = за 3 часа, 2 слесарь - за 4 часа

Замечаем, что перестановки происходят отдельно среди четных чисел и среди нечетных чисел.  Поэтому надо ответить на следующий вопрос: есть k предметов, расставленных в каком-то порядке слева-направо и соответствующим образом занумерованных; меняя местами за одну операцию два соседних предмета, нужно расставить их в том же порядке, но справа-налево. Говоря ученым языком, можно сказать, что сначала у нас не было ни одной инверсии (инверсия - это когда предмет с меньшим номером стоит правее предмета с большим номером), а надо сделать максимальное количество инверсий. Меняя местами соседей, мы каждый раз изменяем количество инверсий на 1. Конечно, нам невыгодно уменьшать количество инверсий, а выгодно - увеличивать. Но в каком порядке производить эту операцию - менять местами соседей - абсолютно непринципиально. Поступим, скажем, так. Поменяем сначала местами первый предмет и второй, затем первый и третий, первый и четвертый, и так далее, наконец, первый и последний. Всё. Первый предмет оказался на нужном месте и больше оттуда никуда сдвигаться не будет. Потребовалось нам для этого, естественно, (k-1) операция. Далее будем передвигать второй предмет до тех пор, пока он не поменяется местами с k-м предметом и  не окажется рядом с первым, но левее первого. На это потребуется (k-2) операции. И так далее. Всего мы насчитаем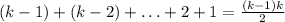 операций.

Остается подвести итоги. Окончательный ответ зависит от того, каково n - четное оно или нечетное.

1-й случай: n - четное, n=2m. Это означает, что у нас m четных чисел и m нечетных чисел. Всего операций получится

2-й случай. n - нечетное, n=2m+1. Это означает, что у нас m четных чисел и (m+1) нечетных чисел.Всего операций получится

Решим задачу для n=5, 6, 7, 23.

n=5 - нечетное;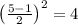

n=6 - четное;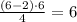

n=7 - нечетное;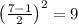

n=23 - нечетное;