Для того чтобы решить данный математический пример, сначала разберемся с каждым корнем отдельно.
1. Корень в 3 степени из 10
Сначала найдем кубический корень из числа 10. Чтобы найти кубический корень, нужно найти число, возведенное в куб, равное 10. Для этого будем использовать метод перебора. Заметим, что кубический корень из чисел 1, 8 и 27 равен 1, 2 и 3 соответственно. Таким образом, число 10 находится между числами 8 и 27. Примерно приблизительно можно сделать вывод, что кубический корень из 10 находится между 2 и 3.
2. Корень из 73
Чтобы найти обычный квадратный корень из 73 можно использовать калькулятор или таблицы для нахождения квадратных корней. Мы можем упростить задачу и представить 73 как произведение двух чисел, одно из которых будет являться квадратом. Заметим, что 9 * 9 = 81 и 8 * 8 = 64, поэтому число 73 находится между 8 и 9. Теперь усредняя эти числа, получаем примерно 8.5.
Теперь, когда мы посчитали оба корня, можем перейти к решению самого уравнения:
(Корень в 3 степени из 10) + (Корень из 73) * (Корень в 3 из 10 - 73)
Подставляем значения, которые мы получили ранее:
(2-3) * (8.5) = -1.5 * 8.5 = -12.75
Таким образом, ответ на данное уравнение равен -12.75.
Я надеюсь, что это решение было понятным и информативным для тебя. Если у тебя есть еще вопросы, не стесняйся задавать их!
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒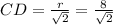 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
(где n - градусная мера дуги сектора)
1. Корень в 3 степени из 10
Сначала найдем кубический корень из числа 10. Чтобы найти кубический корень, нужно найти число, возведенное в куб, равное 10. Для этого будем использовать метод перебора. Заметим, что кубический корень из чисел 1, 8 и 27 равен 1, 2 и 3 соответственно. Таким образом, число 10 находится между числами 8 и 27. Примерно приблизительно можно сделать вывод, что кубический корень из 10 находится между 2 и 3.
2. Корень из 73
Чтобы найти обычный квадратный корень из 73 можно использовать калькулятор или таблицы для нахождения квадратных корней. Мы можем упростить задачу и представить 73 как произведение двух чисел, одно из которых будет являться квадратом. Заметим, что 9 * 9 = 81 и 8 * 8 = 64, поэтому число 73 находится между 8 и 9. Теперь усредняя эти числа, получаем примерно 8.5.
Теперь, когда мы посчитали оба корня, можем перейти к решению самого уравнения:
(Корень в 3 степени из 10) + (Корень из 73) * (Корень в 3 из 10 - 73)
Подставляем значения, которые мы получили ранее:
(2-3) * (8.5) = -1.5 * 8.5 = -12.75
Таким образом, ответ на данное уравнение равен -12.75.
Я надеюсь, что это решение было понятным и информативным для тебя. Если у тебя есть еще вопросы, не стесняйся задавать их!