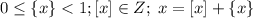В настоящее время на сайте бизнесмена объявлен конкурс по поиску парнерши, информация о ходе которого будет отображаться в реалити-шоу под названием Full Moon Lovers, транслируемом японским стриминговым сервисом AbemaTV. Подать заявку на участие в конкурсе могут девушки от 20 лет, при этом они должны быть оптимистками, «яркими» личностями, стремиться насладиться жизнью на всю катушку и желать мира во всем мире, и , конечно же, быть готовыми отправиться в космический полет.
Отправиться на Луну со своей новой партнершей Маедзава планирует на космическом корабле компании SpaceX — Starship — огромном аппарате, предназначенном для перевозки людей на Луну и Марс. Во время «романтического» путешествия корабль облетит вокруг Луны (не высаживаясь на ее поверхности) и вернется обратно на Землю.
В сентябре 2018 года SpaceX сообщила, что Маедзава выложил внушительную сумму денег, чтобы стать первым частным клиентом Starship после того, как корабль будет готов к путешествиям в космос. И хотя точный размер суммы не сообщался, руководитель SpaceX Илон Маск отметил, что этих средств хватило для частичного финансирования разработок космического корабля.
«Он не бросает слов на ветер», — заявил тогда Маск.
Стоит отметить, что Маедзава оплатил сразу несколько мест на корабле, поскольку, будучи большим поклонником искусства, он собирается взять в полет группу художников, которые должны будут после возвращения на Землю увековечить полученные впечатления в своих произведениях.
Японский миллиардер ищет девушку для путешествия вокруг Луны
Теперь Маедзава решил направить свои силы в другом направлении. 44-летний миллиардер и основатель одного из крупнейших интернет-магазинов в Японии планирует найти свою вторую половинку.
«Поскольку меня все чаще настигает чувство одиночества и пустоты, я задумываюсь об одном: любить одну женщину», — пишет миллиардер-романтик, добавляя, что сначала он стеснялся участвовать в шоу, но теперь действительно надеется встретить свою любовь.
«Вместе с ней я хочу прокричать о нашей любви и мире во всем мире из космоса», — пишет он.
Заявки на участие в конкурсе принимаются до 17 января, начальный отбор будет проведен до конца месяца. В феврале и марте отобранные участники отправятся на первые свидания с Маедзава. Окончательное решение миллиардер должен будет принять уже в конце марта — таким образом, до полета, который предположительно должен состояться в 2023 году, у пары будет достаточно времени, чтобы узнать друг друга.
Тем временем, для того чтобы влюбленные (как и все другие желающие) смогли отправиться в путешествие мечты со SpaceX, необходимо еще много сделать. Компания работает над созданием Starship в течение нескольких последних лет, и за это время достигла определенных успехов — был осуществлен тестовый полет на малых высотах, а в сентябре 2019 года Маск представил миру экспериментальную версию ракеты Starship, заявив, что в 2020 году она совершит первый полет. Однако во время испытаний модели Starship1 произошла нештатная ситуация, после чего SpaceX приняла решение переключиться на другую модель. В декабре Маск сообщил, что первый полет может задержаться на два-три месяца, хотя в отношении долго перспектив его настрой остался оптимистичным.
Даже если полет Starship в этом году состоится, компании предстоит сконструировать много другого оборудования, например, ракетный ускоритель Super Heavy, предназначенный для доставки корабля в открытый космос. И хотя SpaceX заявляет, что миссии на Луну могут стартовать уже в 2022 году, большинство людей считают эти заявления слишком амбициозными.
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение
2)
А значит, если взять (*), . И правда:
(*) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)
А значит, если взять (**), . И правда:
(**) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.
В настоящее время на сайте бизнесмена объявлен конкурс по поиску парнерши, информация о ходе которого будет отображаться в реалити-шоу под названием Full Moon Lovers, транслируемом японским стриминговым сервисом AbemaTV. Подать заявку на участие в конкурсе могут девушки от 20 лет, при этом они должны быть оптимистками, «яркими» личностями, стремиться насладиться жизнью на всю катушку и желать мира во всем мире, и , конечно же, быть готовыми отправиться в космический полет.
Отправиться на Луну со своей новой партнершей Маедзава планирует на космическом корабле компании SpaceX — Starship — огромном аппарате, предназначенном для перевозки людей на Луну и Марс. Во время «романтического» путешествия корабль облетит вокруг Луны (не высаживаясь на ее поверхности) и вернется обратно на Землю.
В сентябре 2018 года SpaceX сообщила, что Маедзава выложил внушительную сумму денег, чтобы стать первым частным клиентом Starship после того, как корабль будет готов к путешествиям в космос. И хотя точный размер суммы не сообщался, руководитель SpaceX Илон Маск отметил, что этих средств хватило для частичного финансирования разработок космического корабля.
«Он не бросает слов на ветер», — заявил тогда Маск.
Стоит отметить, что Маедзава оплатил сразу несколько мест на корабле, поскольку, будучи большим поклонником искусства, он собирается взять в полет группу художников, которые должны будут после возвращения на Землю увековечить полученные впечатления в своих произведениях.
Японский миллиардер ищет девушку для путешествия вокруг Луны
Теперь Маедзава решил направить свои силы в другом направлении. 44-летний миллиардер и основатель одного из крупнейших интернет-магазинов в Японии планирует найти свою вторую половинку.
«Поскольку меня все чаще настигает чувство одиночества и пустоты, я задумываюсь об одном: любить одну женщину», — пишет миллиардер-романтик, добавляя, что сначала он стеснялся участвовать в шоу, но теперь действительно надеется встретить свою любовь.
«Вместе с ней я хочу прокричать о нашей любви и мире во всем мире из космоса», — пишет он.
Заявки на участие в конкурсе принимаются до 17 января, начальный отбор будет проведен до конца месяца. В феврале и марте отобранные участники отправятся на первые свидания с Маедзава. Окончательное решение миллиардер должен будет принять уже в конце марта — таким образом, до полета, который предположительно должен состояться в 2023 году, у пары будет достаточно времени, чтобы узнать друг друга.
Тем временем, для того чтобы влюбленные (как и все другие желающие) смогли отправиться в путешествие мечты со SpaceX, необходимо еще много сделать. Компания работает над созданием Starship в течение нескольких последних лет, и за это время достигла определенных успехов — был осуществлен тестовый полет на малых высотах, а в сентябре 2019 года Маск представил миру экспериментальную версию ракеты Starship, заявив, что в 2020 году она совершит первый полет. Однако во время испытаний модели Starship1 произошла нештатная ситуация, после чего SpaceX приняла решение переключиться на другую модель. В декабре Маск сообщил, что первый полет может задержаться на два-три месяца, хотя в отношении долго перспектив его настрой остался оптимистичным.
Даже если полет Starship в этом году состоится, компании предстоит сконструировать много другого оборудования, например, ракетный ускоритель Super Heavy, предназначенный для доставки корабля в открытый космос. И хотя SpaceX заявляет, что миссии на Луну могут стартовать уже в 2022 году, большинство людей считают эти заявления слишком амбициозными.
По определению,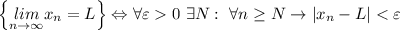
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение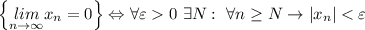
2)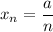
А значит, если взять![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*), 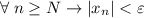 . И правда:
. И правда: 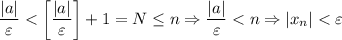
(*) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)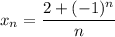
А значит, если взять![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**), 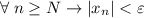 . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда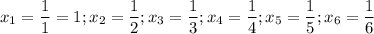
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.