Детская площадка имеет форму прямоугольника, площадь которого равна 170 м2. Одна его сторона на 7 метр(-ов, -а) больше, чем другая. Детской площадке необходимо построить бордюр. В магазине продаётся материал для бордюра в упаковках. В одной упаковке имеется 22 метров(-а) материала. РЕБЯТ
Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:
Из условия следует, что каждый исход равновероятен.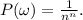
Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок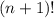
. Теперь можно считать вероятность:
Поскольку а=2,b=-1,c=4, то квадратный трехчлен будет выглядеть таким образом:
2х^2-x+4
2) a)x^2-4x+9
Приравниваем к нолю: x^2-4x+9=0
D=16-36<0, то корней уравнения нет, поэтому разложить на множители невозможно
б)x^2-36
По формуле разница квадратов: x^2-36=(х-6)(х+6)
в)x^2+3x
x^2+3x=0
x^2=-3
x^2≥0, -3<0, поэтому корней нет, разложить на множители невозможно.
г)x^2+4x-5
x^2+4x-5=0
По теореме Виета: х₁=-5,х₂=1
Раскладываем по формуле : ax^2+bx+c=a(x-x₁)(x-x₂)
x^2+4x-5=1(x+5)(x-1)
3.а) x^2-14x+45
x^2-14x+45=0
По т.Виета: x₁=9,x₂=5
Аналогично з.2: x^2-14x+45=(x-9)(x-5)
б)3y^2+7y-6
3y^2+7y-6=0
D=49-4*3*(-6)=49+72=121
√D=11
x₁=(-7+11)/6=2/3
x₂=(-7-11)/6=-3
3y^2+7y-6=3(x-2/3)(x+3)=(3х-2)(х+3)