х² - 3х + у²+ 3 > 0; поскольку число у, возведенное в квадрат больше (или равно при у=0) нуля, то есть число положительное при всех у, то рассмотрим неравенство: х² - 3х + 3 > 0; если оно будет верно, то и верно исходное неравенство х² - 3х + у²+ 3 > 0 x² − 3x + 3 > 0 Сначала решаем квадратное уравнение x² − 3x + 3 = 0. Вот коэффициенты данного квадратного уравнения: a = 1, b = − 3, c = 3. Его дискриминант D = b² − 4ac = (− 3) ² − 4 · 1 · 3 = − 3 Поскольку дискриминант D квадратного уравнения меньше 0, то уравнение не имеет действительных корней, и при любом x левая часть будет либо больше, либо меньше нуля; если a > 0, то при любом х всё выражение будет больше нуля; если a < 0, то при любом х всё выражение будет меньше нуля. В нашем уравнении a=1; > 0, поэтому выражение x² − 3x + 3 всегда будет больше нуля при любом x. Следовательно, наше неравенство x² − 3x + 3 > 0 верно при любом x.
а) 1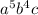7
г) -7
Объяснение:
Одночлен — произведение, состоящее из числового множителя и одной или нескольких переменных, взятых каждая в неотрицательной степени.
Неотрицательные числа - это все положительные числа и 0.
а) 17 - числовой множитель, умноженный на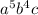
- несколько переменных, каждая из которых в неотрицательной степени: ПОДХОДИТ
б) здесь сумма одночленов: НЕ ПОДХОДИТ
в) -23 - числовой множитель, умноженный на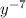
- переменная, взятая в отрицательной степени: НЕ ПОДХОДИТ
г) -7 - числовой множитель, умноженный на переменную в степени 0: ПОДХОДИТ