1) Коэффициент равен , а степень многочлена равна 8.
2) PΔ=7xy³+8x-4y. Степень многочлена равна 4.
3) 4х²+4хz+3x+3z=(x+z)*(4х+3)
Объяснение:
1) Коэффициент при многочлене узнать просто: это вещественное число, стоящее перед множителями хᵃ и уᵇ. Где a, b - степени множителей соответственно х и у. В данном случае коэффициент равен . Теперь, чтобы узнать степень одночлена, надо сложить степени при х и у:
Б
Объяснение:
Пусть А врёт и он отличник. Тогда В тоже воет. Не может быть.
Пусть А врёт и он двоечник. Тогда Г тоже врёт. Опять противоречие.
Значит, А сказал правду.
Пусть Б врёт и он двоечник. Тогда Г говорит правду, и он тоже двоечник. Но двух двоечников быть не может. Противоречие.
Значит, Б тоже сказал правду - он не двоечник.
Пусть Б или хорошист, или троечник.
Значит, врёт или В, или Г.
Если врёт В и он не отличник, тогда отличника вообще нет. Противоречие.
Если врёт Г и он не двоечник, тогда двоечника нет. Опять противоречие.
Единственный возможный вариант - это если Б отличник. Тогда В врёт, что он отличник, а Г говорит правду, что он двоечник.
1) Коэффициент равен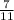
, а степень многочлена равна 8.
2) PΔ=7xy³+8x-4y. Степень многочлена равна 4.
3) 4х²+4хz+3x+3z=(x+z)*(4х+3)
Объяснение:
1) Коэффициент при многочлене узнать просто: это вещественное число, стоящее перед множителями хᵃ и уᵇ. Где a, b - степени множителей соответственно х и у. В данном случае коэффициент равен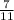
. Теперь, чтобы узнать степень одночлена, надо сложить степени при х и у:
7(степень при х)+1(степень при у)=8.
8 - степень данного одночлена.
2) PΔ=a+b+c=2xy³+3xy³+6x-4y+2xy³+2x=5xy³+6x-4y+2xy³+2x=5xy³+2xy³+6x-4y+2x=7xy³+6x-4y+2x=7xy³+8x-4y.
Степень этого многочлена можно узнать по первому члену. То есть 1 (степень у множителя х)+3(степень у множителя у)=4
3) 4х²+4хz+3x+3z=4x*(x+z)+3*(x+z)=
выносим за скобку множитель (x+z). Получаем
=(x+z)*(4х+3)