1) -0,5x^4=x-4 Можно сделать графически. Левая часть: y = -0,5x⁴ График - квадратичная парабола, ветви направлены вниз. Правая часть: y = x - 4 График - прямая линия, не параллельная осям координат. Пересекает параболу в двух точках. ответ: уравнение имеет 2 действительных корня.
2) y=(x-2)^2+4 на отрезке [0;3] Квадратичная функция, ветви направлены вверх. Наименьшим значением будет вершина параболы. Координаты вершины параболы: х=2 (из уравнения функции), у = 4.
Подставить границы интервала в уравнение функции и выбрать наибольшее: y = (x - 2)² + 4 = (0 - 2)² + 4 = 8 y = (x - 2)² + 4 = (3 - 2)² + 4 = 5
Наибольшее значение функции на отрезке [0; 3] y = 8 в точке x = 3. Наименьшее значение функции на отрезке [0; 3] y = 4 в точке x = 2.
Заметим, что данное неравенство хорошо раскладывается на множители:
Решим неравенство по методу интервалов.
1)
2)
Введем функции и . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, , верно. Так, мы решили это уравнение, получив, что его корень x=2.
Можно сделать графически.
Левая часть: y = -0,5x⁴
График - квадратичная парабола, ветви направлены вниз.
Правая часть: y = x - 4
График - прямая линия, не параллельная осям координат. Пересекает параболу в двух точках.
ответ: уравнение имеет 2 действительных корня.
2) y=(x-2)^2+4 на отрезке [0;3]
Квадратичная функция, ветви направлены вверх. Наименьшим значением будет вершина параболы.
Координаты вершины параболы: х=2 (из уравнения функции), у = 4.
Подставить границы интервала в уравнение функции и выбрать наибольшее:
y = (x - 2)² + 4 = (0 - 2)² + 4 = 8
y = (x - 2)² + 4 = (3 - 2)² + 4 = 5
Наибольшее значение функции на отрезке [0; 3] y = 8 в точке x = 3.
Наименьшее значение функции на отрезке [0; 3] y = 4 в точке x = 2.
Объяснение:
Рассмотрим сначала первое неравенство системы.
Начнем с ОДЗ:
Продолжим решение:
1)
Замена: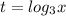 .
.
Обратная замена:
С учетом ОДЗ оба корня подходят.
2)
С учетом ОДЗ получим, что решение неравенства:
Теперь перейдем ко второму неравенству системы:
Понятно, что сначала нужно написать ОДЗ.
Продолжим решение:
Заметим, что данное неравенство хорошо раскладывается на множители:
Решим неравенство по методу интервалов.
1)
2)
Введем функции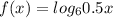 и
и 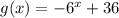 . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно,
. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 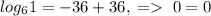 , верно. Так, мы решили это уравнение, получив, что его корень x=2.
, верно. Так, мы решили это уравнение, получив, что его корень x=2.
Тогда решение неравенства с учетом ОДЗ:
Итого имеем:
Найдем пересечение:
Задание выполнено!