Для приема зачета по теории вероятностей преподаватель заготовил 15 задач по вычислению вероятности по классической формуле и 12 задач по формулам сложения и умножения вероятностей. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он умеет решать 10 задач из 15 по первой теме и 8 задач из 12 по второй теме?
Прямые параллельны - это означает, что у них одинаковый угловой коэффициент, то есть одинаковый тангенс угла наклона к оси OX. Иными словами, если мы идем по любой из этих прямых, то сдвинувшись направо, скажем, на 5 единиц, мы поднимемся наверх на одинаковое количество единиц независимо от того, по какой прямой мы двигаемся. Двигаясь по первой прямой из одной отмеченной точки в другую, мы сдвигаемся вправо на 5 единиц и вверх на 2 единицы. А если бы сдвиг направо был бы в два раза больше - на 10 единиц, то вверх мы бы поднялись не на 2 единицы, а на четыре, то есть тоже в два раза больше. Мы видим, что двигаясь уже по второй прямой из одной отмеченной точки в другую, мы поднимаемся вверх на 4 единицы, значит направо мы сдвигаемся на 10 единиц. Значит, p=10.
Если вам скучно было читать мой опус, могу предложить другой веселый. Поскольку тангенс угла наклона первой прямой к оси OX равен 2/5, и прямая пересекает ось OY в точке с координатой 2, эта прямая имеет уравнение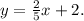
Параллельные прямые имеют одинаковые угловые коэффициенты, значит угловой коэффициент второй прямой равен 2/5. Ось OY вторая прямая пересекает в точке с координатой - 4, поэтому уравнение второй прямой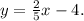
Подставив в это уравнение x=p; y=0, получаем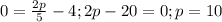 
Если и это рассуждение вас не вдохновило, посмотрите на два треугольника на вашем чертеже. Они, очевидно, подобны, поэтому мы можем записать отношение соответственных сторон: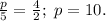
Если и это вас не устраивает, можете придумывать свое решение, а я умываю руки
сгруппируем слагаемые скобками;
= (35a 2+7a 2b 2) + (5b+b 3) =
вынесем за скобки общий множитель первой,
а затем и второй группы;
= 7a 2 • (5+b 2) + b • (5+b 2) =
у нас получилось выражение из двух слагаемых, в каждом
из которых присутствует общий множитель (5+b 2).
Его мы вынесем за скобку;
= (7a 2+b) • (5+b 2) .
Значит:
35a 2+7a 2b 2+5b+b 3 = (7a 2+b) (5+b 2) .
Разложим на множители ещё один многочлен :
10b 2a – 15b 2 – 8аb + 12b + 6а – 9 =
сгруппируем слагаемые скобками;
= (10b 2a – 15b 2) – (8аb – 12b) + (6а – 9) =
вынесем за скобки общий множитель первой,
а затем второй и третьей группы;
= 5b 2 • (2a – 3) – 4b • (2а – 3) + 3 • (2а – 3) =
у нас получилось выражение из трех слагаемых, в каждом
из которых присутствует общий множитель (2а – 3).
Его мы вынесем за скобку;
= (5b 2 – 4b + 3) • (2a – 3) .