1) графический. Нужно найти для каждого уравнения 2 корня, построить 2 прямые, где они пересекутся это и будет решение системы уравнения. 2) Метод подстановки 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2. 3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если то 5) Пары (2; 1) и решения заданной системы уравнений.
ответ: (2; 1) 3)Алгебраическое сложение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу
Итак, для решения примера надо каждое число представить в степени какого-то числа, желательно чтобы было число одно и то же. Объясняю, к примеру, надо представить число 512 как какое-то число в какой-то степени. 512 это у нас 2 в степени 9 (). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=, 128=, 256=, 64=, 4=, 16=, 8=. С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
Далее всё просто. Чтобы возвести число, стоящее в степени, в степень, то нужно показатели степеней перемножить:
Ну а дальше простая математика 2 класса: при умножении чисел с одинаковыми основаниями, но с разными степенями, их степени складываются; при делении - степени вычитаются. Подсчитаем результат в числителе:
2) Метод подстановки 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если то
5) Пары (2; 1) и решения заданной системы уравнений.
ответ: (2; 1)
3)Алгебраическое сложение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу
Если х = 2, то
Таким образом, мы нашли два решения системы:
Итак, для решения примера надо каждое число представить в степени какого-то числа, желательно чтобы было число одно и то же. Объясняю, к примеру, надо представить число 512 как какое-то число в какой-то степени. 512 это у нас 2 в степени 9 (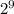 ). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=
). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=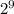 , 128=
, 128=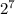 , 256=
, 256=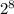 , 64=
, 64=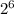 , 4=
, 4=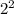 , 16=
, 16=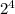 , 8=
, 8=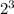 . С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
. С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
Далее всё просто. Чтобы возвести число, стоящее в степени, в степень, то нужно показатели степеней перемножить:
Ну а дальше простая математика 2 класса: при умножении чисел с одинаковыми основаниями, но с разными степенями, их степени складываются; при делении - степени вычитаются. Подсчитаем результат в числителе:
В знаменателе:
И последнее действие:
ответ: 2^{-33}