В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Раскроем скобки (перемножим первую скобку на вторую, т.к между ними подразумевается знак умножения, и раскроем третью скобку, перемножив С поочерёдно на каждое слагаемое в скобке):
-+c+-9c+3--9c
Далее приводим подобные, то бишь выбираем степени с одинаковым показателем (то бишь цифрой над числом/буквой и числа без степеней) и выполняем действия обозначенные перед ними (то бишь, если перед стоит минус, то вычитаем её от другой n*/ В результате остаётся:
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
Раскроем скобки (перемножим первую скобку на вторую, т.к между ними подразумевается знак умножения, и раскроем третью скобку, перемножив С поочерёдно на каждое слагаемое в скобке):
Далее приводим подобные, то бишь выбираем степени с одинаковым показателем (то бишь цифрой над числом/буквой и числа без степеней) и выполняем действия обозначенные перед ними (то бишь, если перед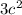
стоит минус, то вычитаем её от другой n*
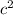/ В результате остаётся:
-17c+3
Подставляем -11 вместо переменной C:
-17*(-11)+3 = 187+3 = 190
Надеюсь не ошибся