Первоначальный прямоугольник имеет размеры х и у 2х + 2у = 36 ⇒ х + у = 18 Теперь можно сказать, что у прямоугольника одна сторона была = х, а другая (18 - х). Площадь его была = х(18 - х) Теперь одну сторону увеличили на 1м ( она стала = х +1) Другую сторону увеличили на 2 ( она стала = 18 - х +2 = 20 - х) Его площадь стала = (х +10)(20 - х) разница в площадях = 30. Составим уравнение : (х + 1)( 20 - х) - х(18 - х) = 30 20х -х² +20 - х -18х + х² = 30 х = 30 - 20 х = 10 (м) - это одна первоначальная сторона сторона другая = 18 - х = 18 - 10 = 8(м)
2х + 2у = 36 ⇒ х + у = 18
Теперь можно сказать, что у прямоугольника одна сторона была = х, а другая (18 - х). Площадь его была = х(18 - х)
Теперь одну сторону увеличили на 1м ( она стала = х +1)
Другую сторону увеличили на 2 ( она стала = 18 - х +2 = 20 - х)
Его площадь стала = (х +10)(20 - х)
разница в площадях = 30. Составим уравнение :
(х + 1)( 20 - х) - х(18 - х) = 30
20х -х² +20 - х -18х + х² = 30
х = 30 - 20
х = 10 (м) - это одна первоначальная сторона сторона
другая = 18 - х = 18 - 10 = 8(м)
1)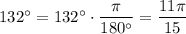
радианная мера дополнение угла 132° до полного: 2π-11π/15 = 19π/15
2) Не сказано какого угла внутреннего или внешнего, поэтому решу для обеих.
а) Внутренний угол многоугольника равен (n-2) · 180° /n, где n - число сторон многоугольника.
(6-2) · 180° /6 = 120° - градусная мера, а радианная мера - 120°π/180°=2π/3
Внешний угол равен 180°-120°=60° - градусная мера, а радианная мера - 60°π/180° = π/3.
б) Аналогично: внутренний угол правильного двенадцатиугольника равен (12-2) · 180° /12 = 150°, а в радианной мере: 150°π/180° = 5π/6
Внешний угол равен 180° - 150° = 30° или 30°π/180° = π/6