Добрые люди это вопрос жизни и смерти 25
​

В решении.

Объяснение:

Формула координат вершины параболы:

х₀ = -b/2a

y₀ = (4ac - b²)/4a, или просто подставить вычисленное значение х₀ в уравнение функции и вычислить значение у₀.

1) у = х² -10х + 20

х₀ =  -b/2a

х₀ = 10/2

х₀ = 5;

у₀ = 5² - 10*5 + 20 = 25 - 50 + 20 = -5.

Координаты вершины параболы (5; -5).  Ветви вверх.

2) y = -x² + 3x - 4

х₀ =  -b/2a

х₀ = -3/-2

х₀ = 1,5;

у₀ = -(1,5)² + 3*1,5 - 4 = -2,25 + 4,5 - 4 = -1,75.

Координаты вершины параболы (1,5; -1,75).  Ветви вниз.

3) у= -х² + 6х - 7

х₀ =  -b/2a

х₀ = -6/-2

х₀ = 3;

у₀ = -(3)² + 6*3 - 7 = -9 + 18 - 7 = 2.

Координаты вершины параболы (3; 2).  Ветви вниз.

4) у = 3х² - 6х + 1

х₀ =  -b/2a

х₀ = 6/6

х₀ = 1;

у₀ = 3*1² - 6*1 + 1 = 3 - 6 + 1 = -2.

Координаты вершины параболы (1; -2).  Ветви вверх.

5) у = -0,2х² + 4х

х₀ =  -b/2a

х₀ = -4/-0,4

х₀ = 10;

у₀ = -0,2*10² + 4*10 = -0,2*100 + 40 = -20 + 40 = 20.

Координаты вершины параболы (10; 20).  Ветви вниз.

1. а) 5xy³*(-2x²y)⁴ = 5xy³*16x⁸y⁴ = 80x¹⁺⁸y³⁺⁴ = 80x⁹y⁷

б) (2y-3x)² - (3x+2y)(2y-3x) = 4y²-12xy+9x²-6xy-9x²+4y²-6xy = 8y²-24xy

2. а) 4ab³-a³b = ab (4b²-a²) = ab (2b-a)(2b+a)

б) -9b-6b²-b³ = -b (9+6b+b²) = -b (b+3)²

3.

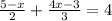
Здесь делаем всем НОЗ: 6.

Теперь, когда у нас стали одинаковые знаменатели, решаем только числитель:

3(5-x)+2(4x-3)-24 = 0

15-3x+8x-6-24 = 0

-3x+8x+15-6-24 = 0

-5x-13 = 0

-5x = 13

x = -2,6

4. Увы, задачу не понял.

5. y = 4x-7 - линейная функция, графиком является прямая.

y = x+83 - линейная функция, графиком является прямая.

Построим таблицы:

1) y = 4x-7

x | 0 1

y | -7 -3

y₁ = 4*0-7 = -7

y₂ = 4*1-7 = -3

2) y = x+83

x | 0 1

y | 83 84

y₁ = 0+83 = 83

y₂ = 1+83 = 84

Как строить координатную плоскость - думаю, не надо объяснять.