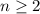Докажем методом математической индукции
1) n = 2: - верно
2) Предположим, что и при верно неравенство
3) Индукционный переход
Очевидно, что и (по предположению), то сложив эти неравенства, получим , т.е. третий пункт выполнено. Следовательно, на основании метода математической индукции делаем вывод, что неравенство верно для всех натуральных
Докажем методом математической индукции
1) n = 2: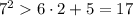 - верно
- верно
2) Предположим, что и при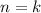 верно неравенство
верно неравенство 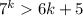
3) Индукционный переход
Очевидно, что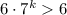 и
и 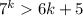 (по предположению), то сложив эти неравенства, получим
(по предположению), то сложив эти неравенства, получим 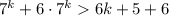 , т.е. третий пункт выполнено. Следовательно, на основании метода математической индукции делаем вывод, что неравенство
, т.е. третий пункт выполнено. Следовательно, на основании метода математической индукции делаем вывод, что неравенство 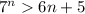 верно для всех натуральных
верно для всех натуральных