Пусть t - время заполнения резервуара 1-ой трубой,тогда (t-12) - время заполнения резервуара 2-ой трубой.
В таких задачах площадь резервуара или обьём(неважно) можно брать за 1. Если брать какую-нибудь букву то она потом всёравно сократится. Просто принято брать за 1.))
Пусть 1 - площадь резервуара, тогда cкорость заполнения резервуара 1-ой трубой, скорость заполнения 2-ой трубой. А двумя трубами вместе - или +. Прировняем:
1.
6sin^2x-3sinx*cosx-cos^2x=sin^2x+cos^2x
5sin^2x-3sinx*cosx-2cos^2x=0 /:cos^2x≠0
5tg^2x-3tgx-2=0
замена tgx=t
5t^2-3t-2=0
t=1
t=-2/5
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-2/5
x=-arctg(2/5)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(2/5)+pik, k∈Z
2.
5sin^2x+3sinx*cosx-2cos^2x=3sin^2x+3cos^2x
2sin^2x+3sinx*cosx-5cos^2x=0 /:cos^2x≠0
2tg^2x+3tgx-5=0
замена tgx=t
2t^2+3t-5=0
t=1
t=-5/2
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-5/2
x=-arctg(5/2)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(5/2)+pik, k∈Z
Пусть t - время заполнения резервуара 1-ой трубой,тогда (t-12) - время заполнения резервуара 2-ой трубой.
В таких задачах площадь резервуара или обьём(неважно) можно брать за 1. Если брать какую-нибудь букву то она потом всёравно сократится. Просто принято брать за 1.))
Пусть 1 - площадь резервуара, тогда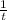
cкорость заполнения резервуара 1-ой трубой,
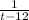скорость заполнения 2-ой трубой. А двумя трубами вместе - 
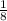или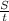 
+
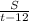. Прировняем:
t=24 - время заполнения 1-ой трубой
t=24-12=12 - время заполнения 2-ой трубой.