cosx= - 1 , х={-3пи/2; 2пи} по фигурным скобкам непонятно, границы интервала включены в интервал или нет. Пусть будут включены. x ∈ [- ; 2π ]
cos x = -1 x = π + 2πn, где n ∈ Z - целое число n = -2 ⇒ x = π - 4π = -3π ⇒ -3π < -3π/2 ⇒ не входит в интервал n = -1 ⇒ x = π - 2π = -π ⇒ -π > -3π/2 ⇒ входит в интервал n = 0 ⇒ x = π ⇒ π < 2π ⇒ входит в интервал n = 1 ⇒ x = π + 2π = 3π ⇒ 3π > 2π ⇒ не входит в интервал
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
x ∈ [-
cos x = -1
x = π + 2πn, где n ∈ Z - целое число
n = -2 ⇒ x = π - 4π = -3π ⇒ -3π < -3π/2 ⇒ не входит в интервал
n = -1 ⇒ x = π - 2π = -π ⇒ -π > -3π/2 ⇒ входит в интервал
n = 0 ⇒ x = π ⇒ π < 2π ⇒ входит в интервал
n = 1 ⇒ x = π + 2π = 3π ⇒ 3π > 2π ⇒ не входит в интервал
ответ: x = -π, x = π
Смотри решение.
Объяснение:
решения (через дискриминант):
Порядок решения:
а. Записываем уравнение в исходном виде;
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
решения (через теорему Виетта):
Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.
Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.
Общая формула квадратного уравнения: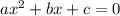
(для справок).
Теперь переходим к решению данного квадратного уравнения: