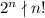Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
honutem
14.07.2021 14:24 •
Алгебра
Доказать, что n! не делится на 2^n (n>=1)
Показать ответ
Ответ:
bizi2002
15.10.2020 15:42
Сравним степени вхождения двойки в
и
. В первом случае, очевидно,
. Во втором:
. Поэтому
0,0
(0 оценок)
Популярные вопросы: Алгебра
facss
06.02.2023 19:08
Довести що для всіх значень x виконується нерівність (x-1)(x-2) (x-2)(x+3)...
danilosipov9997
06.02.2023 19:08
Фермер растил овец и баранов. Весной баранов было 40%40% от общего числа животных. Летом фермер купил несколько баранов, после чего овец стало 20%20%. А осенью он купил несколько овец,...
Влад11737463
12.11.2021 06:40
Как можно быстррее ответ, сделайте первый хотябы...
fotoschoolio
28.12.2020 11:43
2. a) Начертите ÐАОВ; b) внутри угла проведите луч ОС; c) найдите величину угла АОВ, если ÐАОС=120, ÐВОС в 3 раза больше ÐАОС....
89640197456
20.04.2022 08:16
7.2. На рисунке 7.5 укажите равные треугольники....
Keterina0905keka
02.08.2022 13:43
Выполните сложение,вычисление, умножение и деление комплексных чисел z1 и z2 z1=5-i z2=0,5+3l...
T3211
30.12.2022 20:44
Варианты : А)1/y+3 Б)1 В)y^2-9 Г)1/y-3 ответить с объяснением быстрее...
kartew
10.02.2022 21:55
Упрости вырожение (m+n)(m-n+1)-(m-n)(m+n-1)...
ebloock
23.01.2020 09:41
Обьясните как это делать ...
alfa2009
03.09.2022 10:19
Устройство состоит из двух элементов, работающих независимо. вероятности безотказной работы этих элементов равны соответственно 0,75 и 0,9. тогда вероятность того что в течение дня...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Сравним степени вхождения двойки в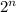 и
и 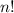 . В первом случае, очевидно,
. В первом случае, очевидно, 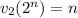 . Во втором:
. Во втором: ![v_{2}(n!)=\sum\limits_{i=1}^{\infty}[\frac{n}{2^{i}}]< \sum\limits_{i=1}^{\infty}\frac{n}{2^{i}}=n](/tpl/images/1358/9881/79b0f.png) . Поэтому
. Поэтому