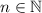Докажем методом математической индукции.
1) База индукции:
2) Предположим, что и для выражение
3) Индукционный переход:
Первое слагаемое делится на 9 по второму пункту и второе слагаемое делится на 9, так как имеет сомножитель 9.
То есть, при
Докажем методом математической индукции.
1) База индукции: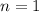
2) Предположим, что и для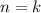 выражение
выражение 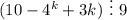
3) Индукционный переход: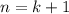
Первое слагаемое делится на 9 по второму пункту и второе слагаемое делится на 9, так как имеет сомножитель 9.
То есть,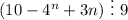 при
при