Рациональное число m/t будет являться корнем уравнения если m делитель а0, а t - делитель аn. (По-моему это следствие из теоремы Безу) Т.к. в нашем случае то если есть рациональные корни, то это числа -1 или 1.
Если х=-1, то -1+p+1=0, т.е. p=0.
Если х=1, то 1-p+1=0, т.е. p=2.
Т.о. при p>2 рациональных корней уравнение не имеет. ч.т.д.
Рациональное число m/t будет являться корнем уравнения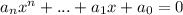 если m делитель а0, а t - делитель аn. (По-моему это следствие из теоремы Безу) Т.к. в нашем случае
если m делитель а0, а t - делитель аn. (По-моему это следствие из теоремы Безу) Т.к. в нашем случае 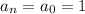 то если есть рациональные корни, то это числа -1 или 1.
то если есть рациональные корни, то это числа -1 или 1.
Если х=-1, то -1+p+1=0, т.е. p=0.
Если х=1, то 1-p+1=0, т.е. p=2.
Т.о. при p>2 рациональных корней уравнение не имеет. ч.т.д.