Доказать что число 5 * 2^(3n-2) + 3^(3n-1) делится на 19
Доказательство:
1) База индукции: n = 1
2) Предположим что и при выражение
3) Индукционный переход: n = k+1
Первое слагаемое делится на 19 по предположению (второй пункт), а второе слагаемое очевидно что делится на 19, так как имеет сомножитель 19.
Доказать что число 5 * 2^(3n-2) + 3^(3n-1) делится на 19
Доказательство:
1) База индукции: n = 1
2) Предположим что и при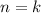 выражение
выражение 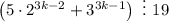
3) Индукционный переход: n = k+1
Первое слагаемое делится на 19 по предположению (второй пункт), а второе слагаемое очевидно что делится на 19, так как имеет сомножитель 19.