За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. Тогда пол оборота по циферблату - оборот на 180°. Пройденный угол минутной стрелки: т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки: т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время между 5ч и 6ч, значит угол, пройденный часовой стрелкой угол, пройденный минутной стрелкой угол между часовой и минутной стрелками
Фиксированная стрелка будильника поставлена на 6 часов. Выразим угол между фиксированной и часовой стрелками будильника:
По условию часовая стрелка делит угол между фиксированной стрелкой будильника и минутной пополам,т.е. углы равны. Решим уравнение: (мин)
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. Тогда пол оборота по циферблату - оборот на 180°. Пройденный угол минутной стрелки: т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки: т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время между 5ч и 6ч, значит угол, пройденный часовой стрелкой угол, пройденный минутной стрелкой угол между часовой и минутной стрелками
Фиксированная стрелка будильника поставлена на 6 часов. Выразим угол между фиксированной и часовой стрелками будильника:
По условию часовая стрелка делит угол между фиксированной стрелкой будильника и минутной пополам,т.е. углы равны. Решим уравнение: (мин)
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. Тогда пол оборота по циферблату - оборот на 180°.
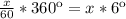
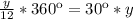
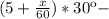 угол, пройденный часовой стрелкой
угол, пройденный часовой стрелкой
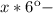 угол, пройденный минутной стрелкой
угол, пройденный минутной стрелкой
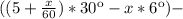 угол между часовой и минутной стрелками
угол между часовой и минутной стрелками
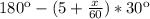
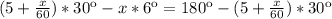
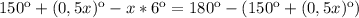
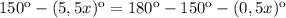
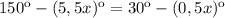
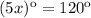
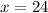 (мин)
(мин)
Пройденный угол минутной стрелки:
т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки:
т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время между 5ч и 6ч, значит
Фиксированная стрелка будильника поставлена на 6 часов.
Выразим угол между фиксированной и часовой стрелками будильника:
По условию часовая стрелка делит угол между фиксированной стрелкой будильника и минутной пополам,т.е. углы равны.
Решим уравнение:
ответ: В) в 5 часов 24 минуты
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. Тогда пол оборота по циферблату - оборот на 180°.
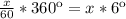
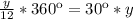
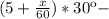 угол, пройденный часовой стрелкой
угол, пройденный часовой стрелкой
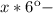 угол, пройденный минутной стрелкой
угол, пройденный минутной стрелкой
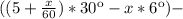 угол между часовой и минутной стрелками
угол между часовой и минутной стрелками
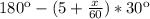
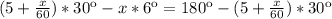
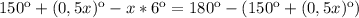
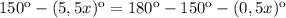
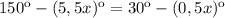
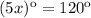
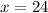 (мин)
(мин)
Пройденный угол минутной стрелки:
т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки:
т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время между 5ч и 6ч, значит
Фиксированная стрелка будильника поставлена на 6 часов.
Выразим угол между фиксированной и часовой стрелками будильника:
По условию часовая стрелка делит угол между фиксированной стрелкой будильника и минутной пополам,т.е. углы равны.
Решим уравнение:
ответ: В) в 5 часов 24 минуты