Докажи тождество: (2x/x+2+4/x^2+5x+6−3|x+3):2x−1/3+x/3+x=1.

В качестве ответа приложи файл с доказательством:

Объяснение:

1)Найти координаты вершины параболы:

а) y=x²-7x+10

   х₀= -b/2a =7/2=3,5

   у₀=3,5²-7*3,5+10=12,25-24,5+10= -2,25

Координаты вершины параболы (3,5; -2,25)

б)y= -2x²+3x+5

    х₀= -b/2a= -3/-4=0,75

    у₀= -2*0,75²+5*0,75+5= -2*0,5625+2,25+5= -1,125+2,25+5=6,125

Координаты вершины параболы (0,75; 6,125)

2)Найти координаты точек пересечения функции с осями координат:

а) y= -x²+5x-1

При пересечении графика с осью У х=0:

х=0

у= -0²+5*0-1

у= -1

Координаты пересечения графика с осью У (0; -1)

Для определения точек пересечения с осью Х (график парабола) нужно решить квадратное уравнение:

-x²+5x-1 =0

х²-5х+1=0

х₁,₂=(5±√25-4)/2

х₁,₂=(5±√21)/2

х₁,₂=(5±4,6)/2

х₁=0,2

х₂=4,8

Координаты точек пересечения графиком оси Х, нули функции,  

(0,2; 0)  (4,8; 0)  

б)y=5x²-7x+2

При пересечении графика с осью У х=0:

х=0

у=5*0²-7*0+2

у=2

Координаты пересечения графика с осью У (0; 2)

Для определения точек пересечения с осью Х (график парабола) нужно решить квадратное уравнение:

5x²-7x+2=0

х₁,₂=(7±√49-40)/10

х₁,₂=(7±√9)/10

х₁,₂=(7±3)/10

х₁=0,4

х₂= 1

Координаты точек пересечения графиком оси Х, нули функции,

(0,4; 0)    (1; 0)

Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии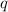 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.

Графически это выглядит так: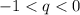 или .

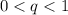Рассмотрим наши примеры:

1)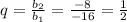 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.

2)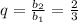 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.

3)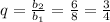 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.