Если один из множителей делится на 10, то и всё произведение делится на 10.
Объяснение:
Очевидно, что полученное выражение делится на 10, что и требовалось доказать.
Если один из множителей делится на 10, то и всё произведение делится на 10.
Объяснение: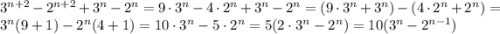
Очевидно, что полученное выражение делится на 10, что и требовалось доказать.