Докажите что для любых натуральных чисел n выполняются условия 1)(n^2+3n) кратно 2 2)n(n+1)^2*(3n=2) кратно 4 3)(n^3+11n) кратно 6 4)(n^3+3n^2+2n) кратно 6
Так как 3 - нечетное число, то один из множителей обязательно будет четным. Если в произведении есть хотя бы один четный множитель, то все произведение делится на 2.
2) Откуда взялся знак равенства?
3) Предположим, что при n=k делится на 6
Докажем что и при n=k+1 предположение верно: - верно
4) Предположим, что при n=k делится на 6Докажем что и при n=k+1 предположение верно: - верно
1)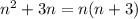
Так как 3 - нечетное число, то один из множителей обязательно будет четным. Если в произведении есть хотя бы один четный множитель, то все произведение делится на 2.
2) Откуда взялся знак равенства?
3) Предположим, что при n=k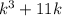 делится на 6
делится на 6
Докажем что и при n=k+1 предположение верно: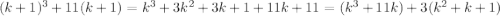 - верно
- верно
4) Предположим, что при n=k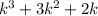 делится на 6Докажем что и при n=k+1 предположение верно:
делится на 6Докажем что и при n=k+1 предположение верно: 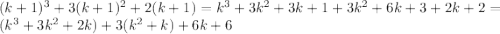 - верно
- верно
n^2+3n=n(n+3)-произведение двух разных по четности слогаемых быдут четным числом. и любое четное(и при том натуральное) число делится на 2.
n(n+1)^2*(3n+2)
Рассмотрим:
1)n(n+1)^2 -это число являеется произведением двух разных по четности чисел -это четное число
2)(3n+2) - это нечетное число
но так как n -натуральное то:
при n=1;
1*(1+1)^2(3*1+2)=4*5=20 -кратно 4
при n=2 :2(2+1)^2(3*2+2)=18*8=144 -кратно 4
значит при всех других натуральных n будет кратно 4