Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается . Для этого нужно понять на какую цифру заканчиваются степени двойки:
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число заканчивается на цифру 4. Следовательно заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
Метод интервалов – простой решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной. Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается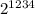 . Для этого нужно понять на какую цифру заканчиваются степени двойки:
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число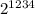 заканчивается на цифру 4. Следовательно
заканчивается на цифру 4. Следовательно 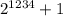 заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».