1. Пусть х - скорость машины на второй половине пути. 45 мин=3/4 часа. (x-15)*1=x*(3/4) x-15=3x/4 x/4=15 x=60 ответ: скорость машины на второй половине пути 60 км/ч. 2. y=3/(5+2*cosx) [π/2;4π/3] y`=(3/(5+2*cosx))`=(3`*(5+2*cosx)-3*(5+2*cosx)`)/(5+2*cosx)=0 -3*(-2*sinx)/(5+2*cosx)²=0 6*sinx=0 sinx=0 x=π y(π)=3/(5+2*cosπ)=3/(5+2*(-1))=3/(5-2)=3/3=1=ymax, y(π/2)=3/(5+2*cos(π/2))=3/(5+2*0)=3/5. y(4π/3)=3/(5+2*cos(4π/3))=3/(5+2*(-sin(π/6))=3/(5+(2*(-1)=3/(5-1)=3/4. ответ: ymax=1. 3. (2*sinx-√2)*√(-cosx)=0 ОДЗ: -cosx>0 cosx<0 x∈(π/2;3π/2) 2*sinx-√2=0 2*sinx=√2 sinx=√2/2 x₁=π/4 ∉ОДЗ x₂=3π/4 ∈ОДЗ √(-cosx)=0 -cosx=0 cosx=0 x₃=π/2 ∈ОДЗ. ответ: x₁=3π/4 x₂=π/2.
Пусть х л - максимальная вместимость ёмкости, тогда x/2 л - это заполнена наполовину водой. После того как в нее добавили еще 210 л, емкость оказалась заполнена на 7/8. Составим уравнение.
560 л - максимальная вместимость ёмкости
ответ: Г
Второй
· Пусть вся ёмкость составляет 1 или же , где х - максимальная вместимость емкости, тогда ёмкость, заполненная водой наполовину представляет собой .
· После того как в нее добавили еще 210 л, емкость оказалась заполнена на 7/8. Представим данную запись.
Пусть х - скорость машины на второй половине пути. 45 мин=3/4 часа.
(x-15)*1=x*(3/4)
x-15=3x/4
x/4=15
x=60
ответ: скорость машины на второй половине пути 60 км/ч.
2.
y=3/(5+2*cosx) [π/2;4π/3]
y`=(3/(5+2*cosx))`=(3`*(5+2*cosx)-3*(5+2*cosx)`)/(5+2*cosx)=0
-3*(-2*sinx)/(5+2*cosx)²=0
6*sinx=0
sinx=0
x=π
y(π)=3/(5+2*cosπ)=3/(5+2*(-1))=3/(5-2)=3/3=1=ymax,
y(π/2)=3/(5+2*cos(π/2))=3/(5+2*0)=3/5.
y(4π/3)=3/(5+2*cos(4π/3))=3/(5+2*(-sin(π/6))=3/(5+(2*(-1)=3/(5-1)=3/4.
ответ: ymax=1.
3.
(2*sinx-√2)*√(-cosx)=0 ОДЗ: -cosx>0 cosx<0 x∈(π/2;3π/2)
2*sinx-√2=0 2*sinx=√2 sinx=√2/2 x₁=π/4 ∉ОДЗ x₂=3π/4 ∈ОДЗ
√(-cosx)=0 -cosx=0 cosx=0 x₃=π/2 ∈ОДЗ.
ответ: x₁=3π/4 x₂=π/2.
Пусть х л - максимальная вместимость ёмкости, тогда x/2 л - это заполнена наполовину водой. После того как в нее добавили еще 210 л, емкость оказалась заполнена на 7/8. Составим уравнение.
560 л - максимальная вместимость ёмкости
ответ: Г
Второй· Пусть вся ёмкость составляет 1 или же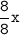
, где х - максимальная вместимость емкости, тогда ёмкость, заполненная водой наполовину представляет собой 
.
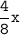· После того как в нее добавили еще 210 л, емкость оказалась заполнена на 7/8. Представим данную запись.
⇒ 210 будет равняться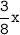
, т.к. 7/8 - 4/8 = 3/8
· Тем самым составим пропорцию.
210 л - 3/8 * x
? л - 8/8 * x
· Или же
210 л - 3/8 * x
? л - 1 * x
· Т.е.
210 л - 3/8 * x
? л - x
А теперь решим пропорцию.
560 л - максимальная вместимость емкости.
ответ: Г