Докажите, что значение выражения является целым числом.

Показать ответ

Ответ:

помидор2324

15.01.2023 18:25

Приравняем правые части:

$\sqrt{x}=-2x+b$

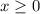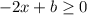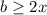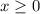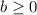Т.к. в левой части арифметический квадратный корень, то $x\geq0$ и $-2x+b\geq0$ , следовательно $b\geq2x$ , а т.к. $x\geq0$ , то и $b\geq0$ .

Теперь возведем обе части в квадрат:

x^2=4x^2-4xb+b^2

Соберем все справа:

3x^2-4xb+b^2=0

Для того, чтобы это уравнение имело корни, нужно чтобы дискриминант был неотрицательным:

D=(-4b)^2-4*4*b^2=0

Следовательно b может быть любым числом, но помня, что b должно быть неотрицательным, получаем ответ:

при любом неотрицательном значении b.

Графики: http://yotx.ru/default.aspx?clr0=000000&exp0=sqrt%28x%29&clr1=666666&exp1=-2x%2b10&mix=-10&max=10&asx=on&u=mm&nx=x&aiy=on&asy=on&ny=y&iw=600&ih=400&ict=png&aa=on

0,0(0 оценок)

Ответ:

vika2069

02.02.2021 00:51

Выполнив деление получим:

$\frac{(2x + 3\sqrt{x} - 2)(5\sqrt{x} - 2x + 3)}{(2 + \sqrt{x})(3 - \sqrt{x})} - 4x$

Введём замену. Пусть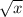 $\sqrt{x}$ = t ≥ 0, тогда x = $t^{2}$ .

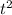Перепишем данное выражение с учётом замены. Получим:

$\frac{(2t^{2} + 3t - 2)(5t - 2t^{2} + 3)}{(2 + t)(3 - t)} - 4x$

Найдём корни всех квадратных трёхчленов в числителе и разложим их на множители:

$2t^{2} + 3t - 2 = 0 \\ D = b^{2} - 4ac = 9 + 16 = 25 \\ x1 = \frac{-3 - 5}{4} = -2 \\ x2 = \frac{-3+5}{4} = 0.5 \\ \\$

Разложение будет иметь вид: 2(t + 2)(t - 0.5)

Аналогично поступаем со вторым:

$-2t^{2} + 5t + 3 = 0 \\ D = b^{2} - 4ac = 25 + 24 = 49 \\ x1 = 3; x2 = -0.5$

Разложение имеет вид: -2(t - 3)(t + 0.5)

Подставим вместо трёхчленов их разложения и проведём некторые преобразования, но оговоримся, что поскольку преобразование идёт лишь при допустимых значениях переменных, то t≥0; t≠3:

$\frac{-4(t+2)(t-0.5)(t-3)(t+0.5)}{(2+t)(3-t)} - 4t^{2} = \frac{-4(t-0.5)(t+0.5)(t-3)}{3-t} - 4t^{2} = \frac{4(t^{2} - 0.25)(3-t)}{3 - t} - 4t^2$ \\ = 4t^{2} - 1 - 4t{2} = -1