Алгебра: Докажите что значения выражения 1) 11^4+11^3 кратно 12

Возьмем две точки , , причем .Им соответствуют значения функции и .Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности : если он положительный, то ; если равен нулю, то значения равны; иначе .По предположению, , поэтому вторая скобка отрицательна.Если , то сумма меньше -16, тогда первая скобка тоже отрицательна, а всё произведение положительно и Получили, что большему значению аргумента соответствует большее значение функции, тогда на отрезке функция возрастает.Аналогично,...

Докажите что значения выражения 1) 11^4+11^3 кратно 12

Показать ответ

Ответ:

urspacce

17.01.2023 05:17

В решении.

Объяснение:

№1

Какая из следующих функций является квадратичной, ее выписать и указать ее коэффициенты:

а) у=х²+2-4х ; б) у=х²+22; в) у=-х-43х г) у=-3х²+27-5х; д) у=2-4х.

Квадратичные функции вида у = ax² + bx + c;

В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, c называется известным или свободным членом.

у=х²+2-4х; первый коэффициент = 1; второй = -4; свободный член = 2;

у=х²+22; первый коэффициент = 1; второй = 0; свободный член = 22;

у=-3х²+27-5х; первый коэффициент = -3; второй = -5; свободный член = 27.

№2

Найти координаты вершины параболы по формуле:

а) у = -х² + 2 - 4х;

б) у = х² + 22х - 3;

в) у = -х - 43х² + 5;

г) у = -3х² + 27 - 5х;

д) у = 12 - 4х².

Формула х₀ = -b/2a; потом значение х₀ подставить в уравнение функции и вычислить у₀. (х₀; у₀) - координаты вершины параболы.

а) у = -х² - 4х + 2;

х₀ = 4/-2

х₀ = -2;

у₀ = -(-2)² - 4 * (-2) + 2 = -4 + 8 + 2 = 6;

у₀ = 6;

Координаты вершины параболы: (-2; 6);

б) у = х² + 22х - 3;

х₀ = -22/2

х₀ = -11;

у₀ = (-11)² + 22 * (-11) - 3 = 121 - 242 - 3 = -124;

у₀ = -124;

Координаты вершины параболы: (-11; -124);

в) у = - 43х² - х + 5;

х₀ = 1/-86

х₀ = -0,01;

у₀ = -43 * (-0,01)² - (-0,01) + 5 = -0,0043 + 0,01 + 5 = 5,0057

у₀ = 5;

Координаты вершины параболы: (-0,01; 5);

г) у = -3х² - 5х + 27;

х₀ = 5/-6

х₀ = -5/6;

у₀ = -3 * (-5/6)² - 5 * (-5/6) + 27 = -25/12 + 25/6 + 27 = 349/12 = 29 1/12;

у₀ = 29 1/12;

Координаты вершины параболы: (-5/6; 29 1/12);

д) у = - 4х² + 12;

х₀ = 0/-8

х₀ = 0;

у₀ = -4 * 0² + 12

у₀ = 12;

Координаты вершины параболы: (0; 12),

№3

Составьте квадратный трехчлен ах²+вх+с, у которого:

а) а=3,в=-12,с=0; → 3х² - 12х;

б) а=1,в=0,с=4; → х² + 4;

в) а=-1,в=-1,с=114; → -х² - х + 114;

г)а=2,в=-1,с=0,5; → 2х² - х + 0,5;

д) а=-13,в=10,с=20; → -13х² + 10х + 20.

0,0(0 оценок)

Ответ:

driftsmuk1

14.02.2021 08:10

Возьмем две точки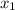 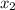x_1 , x_2 , причем x_1 .

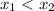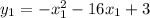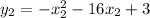Им соответствуют значения функции y_1=-x_1^2-16x_1+3 и y_2=-x_2^2-16x_2+3 .

Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности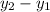 y_2-y_1 : если он положительный, то 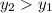y_2y_1 ; если равен нулю, то значения равны; иначе y_1 .

$y_2-y_1=(-x_2^2-16x_2+3)-(-x_1^2-16x_1+3)=\\=(x_1^2-x_2^2)+16(x_1-x_2)=(x_1+x_2)(x_1-x_2)+16(x_1-x_2)=\\=(x_1+x_2+16)(x_1-x_2)$

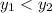По предположению,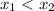 x_1 , поэтому вторая скобка отрицательна.

Если

, то сумма x_1+x_2

меньше -16, тогда первая скобка тоже отрицательна, а всё произведение положительно и y_2y_1.

Получили, что большему значению аргумента соответствует большее значение функции, тогда на отрезке $(-\infty,-8]$ функция возрастает.Аналогично, для $-8\leqslant x_1$ произведение отрицательно. Здесь большему значению аргумента соответствует меньшее значение значение функции, по определению это значит, что функция убывает.