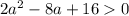Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
10д
17.12.2020 22:16 •
Алгебра
Докажыте неравенство 2a^2-8a+16> 0;
Показать ответ
Ответ:
Yuliya12222222222
08.10.2020 21:54
Квадрат числа всегда > 0, 8 тоже > 0, значит, всё выражение > 0, что и требовалось доказать.
0,0
(0 оценок)
Ответ:
nataliamakarov3
08.10.2020 21:54
Так как
, то
, а значит,
0,0
(0 оценок)
Популярные вопросы: Алгебра
minohbli2207
26.09.2020 03:11
Какие выражения можно записать проще 3^5+2^5 3^5+3^4 3^5×2^5 3^5×2^4 3^5÷2^5 3^5÷2^4 (3^5)^4...
Срочноооооопжлст
14.07.2020 03:34
Решить матрица а= 3 -1 -1 2 в= 1 1 3 1...
солнышко267
14.07.2020 03:34
Решите систему уравнений: x/5+y/6=−9/10 x/8−y/7=−73/56 (/ - это дробь)...
ПоЛИнА10571
14.07.2020 03:34
Вынесете множитель из под знака √25a^7...
приветпрррррр20246р
14.07.2020 03:34
Какие из пар чисел (8; 0); (-5; 5; 3) являются решениями уравнения 5y-2x=26...
caramelka05
19.01.2023 02:44
X-2x²=0 решите уравнения . 2x²+8x=0...
Marik19782002
19.01.2023 02:44
Найдите координаты точек пересечения с осью оx прямых, являющихся графиками уравнений 1) x+y=8; 2)y-x=7...
alexsey13
13.10.2020 02:24
2х-у=3 х-у=6 решите систему уравнений...
elisavetafolst
13.10.2020 02:24
Постройте график линейной функции y= -2x+1. с графика найдите: а) наибольшее и наименьшее значение функции на отрезке [-1; 2]. б)определите, возрастает или убывает функция....
Денис121009
13.10.2020 02:24
Решите неравенство 1,3x-2 2x-0,6...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Квадрат числа всегда > 0, 8 тоже > 0, значит, всё выражение > 0, что и требовалось доказать.
Так как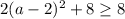 , то
, то 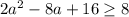 , а значит,
, а значит,