Давайте я вам объясню. Координаты, имеют вид (x;y), то есть, если дана некая функция, в нашем случае игрек зависит от икса. Нам требуется лишь подставить значение икса в координате, и посмотреть, будет ли координата игрека равна координате игрека данной функции. Сейчас вы поймете: Мы берем точку А (2;-1), и что бы проверить, проходит ли функция через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
Отсюда следует, что функция проходит через данную точку.
Данную операцию можно проделать и 2 задании, но зачем? Мы уже итак знаем что при х=2, у=-1. А значит, что функция не проходит через точку В.
1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма .
И правда. Пусть - сумма всех комбинаций по 1 ... по k элементов. Тогда
Т.к. числа отрицательны, то
Если хотя бы одно из , вся сумма равна -1.
В остальных случаях - всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что .
Мы берем точку А (2;-1), и что бы проверить, проходит ли функция
Отсюда следует, что функция проходит через данную точку.
Данную операцию можно проделать и 2 задании, но зачем? Мы уже итак знаем что при х=2, у=-1.
А значит, что функция не проходит через точку В.
1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма
.
И правда. Пусть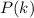
- сумма всех комбинаций по 1 ... по k элементов. Тогда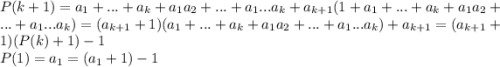 
Т.к. числа отрицательны, то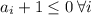
Если хотя бы одно из
, вся сумма равна -1.
В остальных случаях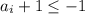
- всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что 
.
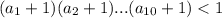А тогда сумма могла равняться только -1