На числовой прямой:
t и -t
Числа имеют противоположные знаки и |t| = |-t|. Точки симметричны относительно нуля.
t и
k=0 ⇒ точки совпадают.
k<0 ⇒ t правее t+2πk на 2πk
k>0 ⇒ t левее t+2πk на 2πk.
t и t+π
t левее t+π на π.
t+π и t-π
t+π правее t-π на 2π.
На числовой окружности:
Точки симметричны относительно оси абсцисс (Ox).
Точки совпадают т.к. 2π это целый круг.
Точки симметричны относительно начала координат т.к. π это половина круга.
Точки совпадают т.к. они различаются на 2π, а это целый круг.
На числовой прямой:
t и -t
Числа имеют противоположные знаки и |t| = |-t|. Точки симметричны относительно нуля.
t и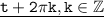
k=0 ⇒ точки совпадают.
k<0 ⇒ t правее t+2πk на 2πk
k>0 ⇒ t левее t+2πk на 2πk.
t и t+π
t левее t+π на π.
t+π и t-π
t+π правее t-π на 2π.
На числовой окружности:
t и -t
Точки симметричны относительно оси абсцисс (Ox).
t и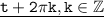
Точки совпадают т.к. 2π это целый круг.
t и t+π
Точки симметричны относительно начала координат т.к. π это половина круга.
t+π и t-π
Точки совпадают т.к. они различаются на 2π, а это целый круг.
Доказать: a/b + b/a >2
Доказательство:
a/b + b/a >2
a/b + b/a - 2 >0
(Общий знаменатель равен ab)
(a² + b² - 2ab)/(ab) >0
(a-b)²/(ab) > 0
a>0, b>0 => ab>0
a≠b, a>0, b>0 => (a-b)²>0
Частное двух положительных чисел является положительным числом,
следовательно, (a-b)²/(ab) > 0
Т.к. неравенство (a-b)²/(ab) >0 было получено из исходного в результате тождественных преобразований, то верно и исходное неравенство.
Таким образом, получаем: a/b + b/a >2
Что и требовалось доказать