Доведідь що при будь-якому натуральному n виконується рівність :
1•2+2•3+3•4++n(n+1)=n(n+1)(n+2)
3

Question

Алгебра: Доведідь що при будь-якому натуральному n виконується рівність : 1•2+2•3+3•4++n(n+1)=n(n+1)(n+2) 3

fagsfssfs · Answer

В первой скобке это сумма квадратов натуральных чисел, для нее известная формула есть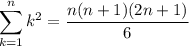 , а вторая скобка это арифметическая прогрессия с первым членом 1 и d = 1...