Приравнять к нулю и решить как квадратное уравнение:
-5х² - 11х - 6 = 0/-1
5х² + 11х + 6 = 0
D=b²-4ac =121 - 120 = 1 √D=1
х₁=(-b-√D)/2a
х₁=(-11-1)/10
х₁= -12/10
х₁= -1,2;
х₂=(-b+√D)/2a
х₂=(-11+1)/10
х₂= -10/10
х₂= -1.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вниз, парабола пересекает ось Ох при х= -1,2 и х= -1, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у >= 0 (как в неравенстве) при значениях х от -1,2 до х= -1.
Решение неравенства: х∈ [-1,2; -1].
Неравенство нестрогое, скобки квадратные.
д) 9х² - 12х + 4 > 0
Приравнять к нулю и решить как квадратное уравнение:
9х² - 12х + 4 = 0
D=b²-4ac =144 - 144 = 0 √D=0
х=(-b±√D)/2a
х=(12±0)/18
х=12/18
х=2/3.
Уравнение имеет один корень, это означает, что парабола не пересекает ось Ох, а "стоит" на ней, ветви направлены вверх.
у > 0 (как в неравенстве) влево и вправо от значения х = 2/3.
Решение неравенства (-∞; 2/3)∪(2/3; +∞).
Неравенство строгое, скобки круглые.
е) 4х² - 12х + 9 <= 0
Приравнять к нулю и решить как квадратное уравнение:
D=b²-4ac =144 - 144 = 0 √D=0
х=(-b±√D)/2a
х=(12±0)/8
х=12/8
х=1,5.
Уравнение имеет один корень, это означает, что парабола не пересекает ось Ох, а "стоит" на ней, ветви направлены вверх.
Находим по графику значения х, при которых у<=0 (как в неравенстве).
у < 0 не существует, так как парабола выше оси Ох, а у = 0 при х = 1,5.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть , где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
В решении.
Объяснение:
Решить неравенства:
г) -5х² - 11х - 6 >= 0
Приравнять к нулю и решить как квадратное уравнение:
-5х² - 11х - 6 = 0/-1
5х² + 11х + 6 = 0
D=b²-4ac =121 - 120 = 1 √D=1
х₁=(-b-√D)/2a
х₁=(-11-1)/10
х₁= -12/10
х₁= -1,2;
х₂=(-b+√D)/2a
х₂=(-11+1)/10
х₂= -10/10
х₂= -1.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вниз, парабола пересекает ось Ох при х= -1,2 и х= -1, отметить эти точки схематично, смотрим на график.
По графику ясно видно, что у >= 0 (как в неравенстве) при значениях х от -1,2 до х= -1.
Решение неравенства: х∈ [-1,2; -1].
Неравенство нестрогое, скобки квадратные.
д) 9х² - 12х + 4 > 0
Приравнять к нулю и решить как квадратное уравнение:
9х² - 12х + 4 = 0
D=b²-4ac =144 - 144 = 0 √D=0
х=(-b±√D)/2a
х=(12±0)/18
х=12/18
х=2/3.
Уравнение имеет один корень, это означает, что парабола не пересекает ось Ох, а "стоит" на ней, ветви направлены вверх.
у > 0 (как в неравенстве) влево и вправо от значения х = 2/3.
Решение неравенства (-∞; 2/3)∪(2/3; +∞).
Неравенство строгое, скобки круглые.
е) 4х² - 12х + 9 <= 0
Приравнять к нулю и решить как квадратное уравнение:
D=b²-4ac =144 - 144 = 0 √D=0
х=(-b±√D)/2a
х=(12±0)/8
х=12/8
х=1,5.
Уравнение имеет один корень, это означает, что парабола не пересекает ось Ох, а "стоит" на ней, ветви направлены вверх.
Находим по графику значения х, при которых у<=0 (как в неравенстве).
у < 0 не существует, так как парабола выше оси Ох, а у = 0 при х = 1,5.
Решение неравенства {1,5}.
Решение единичное, скобки фигурные.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть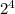 , где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
, где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов: