1) вероятность того, что взятое изделие окажется высшего сорта = 0.8, значит вероятность обратного утверждения (что взятое изделие не окажется высшего сорта) =1-0.8=0.2
Взяли три изделия - вероятность того, что каждое из них в отдельности не окажется высшего сорта, равна 0.2. Значит вероятность того, что все три одновременно (то есть одно не окажется, второе не окажется и третье не окажется) = 0.2*0.2*0.2=0.008
2) Взяли два изделия. Нас устроит любой из двух вариантов:
A) первое высшего сорта, второе - нет
B) первое не высшего сорта, второе - высшего.
Вероятность A = 0.8*0.2=0.16
Вероятность B = 0.2*0.8=0.16
Нас устроит любой из этих исходов, значит нужно рассматривать "сумму" этих событий, а вероятность суммы событий равна сумме вероятностей, то есть 0.16+0.16=0.32
График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.
Заданная первообразная -
Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.
ОТВЕТ: -5.
По условию
Заданная первообразная -
Решим уравнение
Однако вспоминаем про ограничение для самой переменной: (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение
1) 0.008
2) 0.32
Объяснение:
1) вероятность того, что взятое изделие окажется высшего сорта = 0.8, значит вероятность обратного утверждения (что взятое изделие не окажется высшего сорта) =1-0.8=0.2
Взяли три изделия - вероятность того, что каждое из них в отдельности не окажется высшего сорта, равна 0.2. Значит вероятность того, что все три одновременно (то есть одно не окажется, второе не окажется и третье не окажется) = 0.2*0.2*0.2=0.008
2) Взяли два изделия. Нас устроит любой из двух вариантов:
A) первое высшего сорта, второе - нет
B) первое не высшего сорта, второе - высшего.
Вероятность A = 0.8*0.2=0.16
Вероятность B = 0.2*0.8=0.16
Нас устроит любой из этих исходов, значит нужно рассматривать "сумму" этих событий, а вероятность суммы событий равна сумме вероятностей, то есть 0.16+0.16=0.32
Заданная первообразная -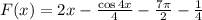
ОТВЕТ: 0.
График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.
Заданная первообразная -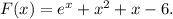
Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.
ОТВЕТ: -5.
По условию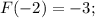
Заданная первообразная -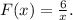
Решим уравнение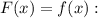
Однако вспоминаем про ограничение для самой переменной: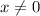 (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение
(о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение 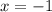
ОТВЕТ: {-1}.