Доярка разливает молоко по всем бидонам. Она распределила молоко поровну по всем бидонам. Неожиданно принесли еще один пустой бидон, и она опять перераспределила молоко поровну, но теперь в каждом бидоне оказалось на 15л меньше, чем в раз. Когда принесли еще один бидон, молоко снова перераспределили, опять везде поровну, но в этот раз на 9л меньше. Сколько литров молока было у доярки?
обозначим общее кол-во молока - M
кол-во начальное бидонов - b
кол-во налитого молока в каждый бидон - х
Тогда M = b * x
После первого дополнительного бидона
бидонов на 1 больше, молока на 15 меньше - общее не изменилось
M = (b + 1)(x - 15)
После второго дополнительного бидона
бидонов еще на 1 больше, молока еще на 9 меньше - общее не изменилось
M = (b + 1 + 1 )(x - 15 - 9) = (b + 2)(x - 24)
получаем систему
bx = (b + 1)(x - 15)
bx = (b + 2)(x - 24)
---
bx = bx - 15b + x - 15
bx = bx - 24b + 2x - 48
-15b + x - 15 = 0
-24b + 2x - 48 = -12b + x - 24 = 0
x = 15 + 15b
x = 12b + 24
---
15 + 15b = 12b + 24
3b = 9
b = 3
нашли кол-во бидонов начальное - 3
x = 15 + 15b = 15 + 45 = 60 кол-во налитого молока в каждый бидон
M = b * x = 60 * 3 = 180
ответ 180 литров
Пусть первоначально было х литров молока и n бидонов.
Так как молоко было распределено поровну, то значит в каждом бидоне было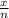 литров молока
литров молока
Изменение ситуации: х литров молока и (n+1) бидонов.
Так как молоко было распределено поровну, то значит в каждом бидоне было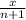 литров молока
литров молока
Оказалось, что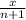 на 15 л меньше, чем
на 15 л меньше, чем 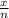
Первое уравнение: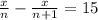
Когда принесли еще один бидон, то ситуация изменилась:
х литров молока и (n+2) бидонов.
Так как молоко было распределено поровну, то значит в каждом бидоне было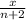 литров молока
литров молока
Оказалось, что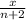 на 9 л меньше, чем
на 9 л меньше, чем 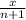
Второе уравнение: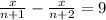
Решаем систему двух уравнений с двумя неизвестными:
Вычитаем из первого второе:
D=16
n=3
x=15·3·4=180
О т в е т. 180 л молока было