Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть, .
ответ: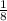
Объяснение:
Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть,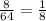 .
.
10 (км/час) - скорость катера в стоячей воде
Объяснение:
х - скорость катера в стоячей воде
х+2 - скорость катера по течению
х-2 - скорость катера против течения
Сейчас определимся со временем:
вышел в 13.00, вернулся в 19.30, был в пути 6,5 часов.
Но 2 часа 45 минут он ждал, это 2 и 45/60=2,75 часа.
Значит, в пути катер находился 6,5-2,75=3,75 часа, уравнение:
18/(х+2) - время по течению
18/(х-2) - время против течения
18/(х+2)+18/(х-2)=3,75 Избавляемся от дробного выражения, общий знаменатель (х+2)(х-2) или х²-4, надписываем над числителями дополнительные множители:
18(х-2)+18(х+2)=3,75(х²-4)
18х-36+18х+36=3,75х²-15
-3,75х²+36х+15=0
3,75х²-36х-15=0/3,75
х²-9,6х-4=0
х₁,₂=(9,6±√92,16+16)/2
х₁,₂=(9,6±√108,16)/2
х₁,₂=(9,6±10,4)/2
х₁= -0,4 отбрасываем, как отрицательный
х₂= 10 (км/час) - скорость катера в стоячей воде
Проверка:
18 : 12=1,5 (часа) - время по течению
18 : 8=2,25 (часа) - время против течения
1,5+2,25+2,75 (остановка)=6,5 (часа) в пути, всё верно.